1º Resolver a equação :

2ºResolver a equação :
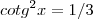
Depois tenho que representar no circulo trigonométrico.
Obrigado pessoal.


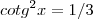

jaegger escreveu:Olá todo mundo, de alguns exercicios de trigo, tenho 2 que não consigo resolver, sera que alguém me consegue ajudar?
1º Resolver a equação :
2ºResolver a equação :
Depois tenho que representar no circulo trigonométrico.

![cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0 cos^2(x+2pi/3)-sin^2(x+2pi/3)=0
[cos(x+2pi/3)-sin(x+2pi/3)][cos(x+2pi/3)+sin(x+2pi/3)]=0
cos(x+2pi/3)-sin(x+2pi/3)=0 ou cos(x+2pi/3)+sin(x+2pi/3)=0](/latexrender/pictures/27ece87d5f7aa42b3dc24e242885bf9d.png)
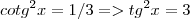 , será que devo pegar com
, será que devo pegar com 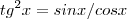 ?
?
jaegger escreveu:Bem, para o 1º tentei :
mas depois não lhe sei dar a volta.
Para o segundo sei que, será que devo pegar com
?
Sera que assim vou la´?
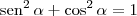 , podemos escrever que:
, podemos escrever que: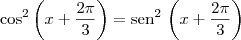
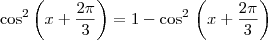
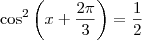
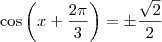
![[0, 2\pi] [0, 2\pi]](/latexrender/pictures/55a5896fe18d9a8d28b6903719b4e376.png) , sabemos que
, sabemos que 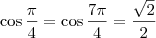 e
e 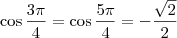 . Temos então quatro possibilidades:
. Temos então quatro possibilidades: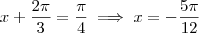 ;
;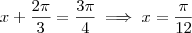 ;
;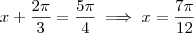 ;
;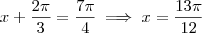 ;
;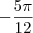 é o mesmo que o ângulo
é o mesmo que o ângulo 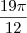 , podemos dizer que a solução (em ordem crescente) da equação é dada por
, podemos dizer que a solução (em ordem crescente) da equação é dada por 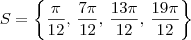 . Agora tente esboçar essa solução no círculo trigonométrico.
. Agora tente esboçar essa solução no círculo trigonométrico.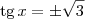 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante