 por leosniper » Ter Mai 08, 2012 18:11
por leosniper » Ter Mai 08, 2012 18:11
Gostaria de saber o conjunto imagem da função f(x) = 3 sen 2x
Sei que os valores máximos do raio devem ser colocados, sendo eles +1 e -1, o resultado deve ser +3 e -3, porém não sei o por que desses valores, se puderem confirmar o período também agradeço
Período = 2 PI/2
Período = PI
-
leosniper
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 08, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Mai 12, 2012 14:42
por MarceloFantini » Sáb Mai 12, 2012 14:42
Primeiramente, não é raio, é amplitude. A função seno é uma função limitada que oscila entre os valores 1 e -1. Ao multiplicá-la por uma constante, você também multiplica a amplitude. O período da função seno é
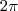
, logo
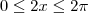
. Trabalhe a partir disso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjunto imagem
por manuoliveira » Dom Jun 20, 2010 22:08
- 1 Respostas
- 2860 Exibições
- Última mensagem por Molina

Qua Jun 23, 2010 21:12
Trigonometria
-
- Conjunto imagem
por Jonatan » Qui Jul 08, 2010 01:47
- 3 Respostas
- 2902 Exibições
- Última mensagem por Tom

Qui Jul 08, 2010 12:58
Funções
-
- [Integral Dupla] Imagem do conjunto S - Mudança de Variável
por neymeirelles » Qua Mai 23, 2012 21:14
- 2 Respostas
- 2693 Exibições
- Última mensagem por neymeirelles

Sex Mai 25, 2012 12:18
Cálculo: Limites, Derivadas e Integrais
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2237 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
-
- Período e imagem
por David Soni » Qua Nov 25, 2009 10:33
- 1 Respostas
- 3210 Exibições
- Última mensagem por Molina

Qua Nov 25, 2009 14:28
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


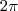 , logo
, logo 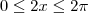 . Trabalhe a partir disso.
. Trabalhe a partir disso.



 , avisa que eu resolvo.
, avisa que eu resolvo.

