 por Kleveland Cristian » Ter Mai 01, 2012 15:14
por Kleveland Cristian » Ter Mai 01, 2012 15:14
Boa tarde a todos!!!! Minha dúvida é quanto a resposta da quetão a seguir:
Qual o menor valor de 3/2-cosx, com x ? [0,2 ?] ?
Minha resolução:
Menor valor de cosseno => (-1)
Substituindo:
3/ 2 - (-1)
3/ 2 + 1
3/ 3
1
O menor valor é 1.
Gostaria de saber se o cálculo e a resposta estão corretos e, caso não, quais seriam?
Grato por quem me ajudar.
-
Kleveland Cristian
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Abr 30, 2012 12:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 16:49
por fraol » Ter Mai 01, 2012 16:49
1) As contas estão incorretas:
3/ 2 - (-1)
3/ 2 + 1
3/ 3
( aqui, pois
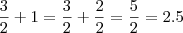
)
2) Se a pergunta é qual é o menor valor de:
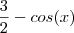
. Então você analisaria a expressão quando o valor de

é máximo e não mínimo como foi feito.
Ok?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cosseno
por karen » Ter Nov 27, 2012 13:17
- 1 Respostas
- 1569 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 19:24
Trigonometria
-
- Cosseno (FUVEST)
 por Ananda » Sex Mar 14, 2008 22:37
por Ananda » Sex Mar 14, 2008 22:37
- 4 Respostas
- 6412 Exibições
- Última mensagem por Ananda

Seg Mar 17, 2008 17:28
Geometria Espacial
-
- Função Cosseno
por DanielFerreira » Qui Jul 30, 2009 17:41
- 1 Respostas
- 2877 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:01
Trigonometria
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4663 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18829 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


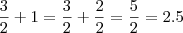 )
)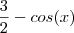 . Então você analisaria a expressão quando o valor de
. Então você analisaria a expressão quando o valor de  é máximo e não mínimo como foi feito.
é máximo e não mínimo como foi feito.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.