 por Nana_3000 » Sex Dez 23, 2011 10:09
por Nana_3000 » Sex Dez 23, 2011 10:09
Olá pessoal do fórum!
Estou com intensas dúvidas sobre equação trigonométrica simples.
Neste caso, como faço para calcular sen 4x = -1, no intervalo de 0 =< x =< 90 graus?
Tentei calcular 4x = -1 => x = -1/4... Então teremos sen -1/4? Como faço para chegar no resultado?
-
Nana_3000
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 23, 2011 09:59
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
 por fraol » Sex Dez 23, 2011 17:25
por fraol » Sex Dez 23, 2011 17:25
Olá Nana,
O caminho
não é fazer

. Tente ler essa equação da seguinte forma:
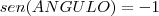
onde o
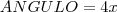
.
Então o que está sendo pedido é que se encontre todos os

, entre 0 e 90 graus, para os quais os ângulos iguais a

tenham o seno igua a

.
Veja se você consegue evoluir o desenvolvimento encontrando, primeiramente, quais são os ângulos que têm seno igual a

e depois achando os

pedidos.
Abç,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Sex Dez 23, 2011 21:18
por MarceloFantini » Sex Dez 23, 2011 21:18
Sugestão: faça
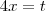
, portanto se
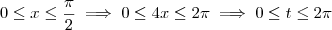
. Então teremos
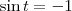
. Encontre t e volte para descobrir x.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Nana_3000 » Sex Dez 23, 2011 22:01
por Nana_3000 » Sex Dez 23, 2011 22:01
Olá Fraol!
Agradeço a força!
Bem, consegui evoluir sim com as explicações dadas por você! Ainda assim, não sei se fui pelo caminho certo de modo a chegar no correto resultado. Mas vamos lá:
1- de acordo com intervalo dado (0 =< x =< 90°), verifiquei, antes de mais nada, quais eram os ângulos correspondentes ao seno = -1, esquematizando o círculo trigonométrico. Como padrão, os valores máximos dentro do mesmo são de -1 a 1. Mas o esquesito é que o valor máximo para o seno do 1° quadrante é 1 e não -1. Logo, um dos valores correspondentes a X com o seno = 1 seria o angulo 90º. Então para a equação seno 4x = -1 nesse intervalo teria uma solução vazia S = {}?
2 - tentei calcular sen 4x = 1. Se um dos valores é 90º, então 90º = 4x => 90°/ 4 = 22,5° (pi / 8 rad)
3 - se o sen do angulo notável 30° = 1/2, então o sen 22,5° é menor do que esse valor. Logo, verifiquei quantas vezes esse mesmo ângulo se repetia no intervalo dado no exercício e estava próximo de 90°. Segundo minha lógica, o angulo se repetia 3 vezes, totalizando 67,5°(ou 3 pi / 8 rad)
Esse raciocínio está correto ou a solução seria mesmo vazia?
Obrigado! (desculpas por não demonstrar corretamente em radianos. No dispositivo que estou respondendo há problemas com o editor de formulas que o fórum oferecem).
-
Nana_3000
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 23, 2011 09:59
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
 por Nana_3000 » Sex Dez 23, 2011 22:04
por Nana_3000 » Sex Dez 23, 2011 22:04
Olá Marcelo!
Não consegui visualizar sua mensagem antes de postar a resposta ao Fraol. Bem, consegui resolver como acima. Consegue identificar se a solução está correta?
Obrigado!
-
Nana_3000
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 23, 2011 09:59
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
 por MarceloFantini » Sex Dez 23, 2011 23:02
por MarceloFantini » Sex Dez 23, 2011 23:02
Sua resposta está errada, e o raciocínio também. Veja que o arco dado é 4x, e não x. Reveja minha sugestão e trabalhe com isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Sex Dez 23, 2011 23:23
por fraol » Sex Dez 23, 2011 23:23
Como o Marcelo disse, o raciocínio não está certo.
Um forma intuitiva de você chegar à resposta certa é preencher as lacunas abaixo, assim ficará mais fácil de visualizar o raciocínio que o Marcelo e eu colocamos.
Responda qual é o primeiro ângulo do círculo trigonométrico cujo seno é igual a -1? ______ graus.
Divida esse valor por 4, afinal esse ângulo vale

e encontrará ______ graus.
Veja que a coincidência com o seu resultado (3) não valida o raciocínio que você desenvolveu.
Resumindo:
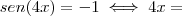
_____ graus


_____ / 4, logo

______ graus.
Boa sorte,
Francisco.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Nana_3000 » Sáb Dez 24, 2011 00:38
por Nana_3000 » Sáb Dez 24, 2011 00:38
Olá Fraol e Marcelo!
Obrigado novamente pela ajuda!
Puxa, era mais fácil do que eu imagina! O problema é que me limitei ao intervalo dado pelo exercício. Agora descobri que apenas o valor final implicava no intervalo em questao. Foi apenas falta de atenção! Pensava que o angulo a ser identificado primeiramente no círculo trigonométrico pelo valor do seno era o válido.
Conforme as instruções do Fraol consegui resolver tal questão:
Responda qual é o primeiro ângulo do círculo trigonométrico cujo seno é igual a -1? 270 graus.
Divida esse valor por 4, afinal esse ângulo vale e encontrará 67,5 graus.
Agora sim isso resolve outras dúvidas referentes às equações trig. simples!
Muito obrigado pela ajuda pessoal!
Resumindo: _____ graus _____ / 4, logo ______ graus.
.
-
Nana_3000
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 23, 2011 09:59
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Informática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- dUVIDA SOBRE EQUAÇAO TRIGONOMETRICA!
por Kevin21 » Qua Set 01, 2010 22:03
- 1 Respostas
- 2948 Exibições
- Última mensagem por VtinxD

Sáb Out 23, 2010 02:51
Trigonometria
-
- [Integral trigonometrica] - Dúvidas
por rafiusk » Qui Out 04, 2012 18:05
- 8 Respostas
- 3699 Exibições
- Última mensagem por rafiusk

Sáb Out 06, 2012 18:22
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Trigonométrica] Dúvidas.
por rafiusk » Dom Out 07, 2012 00:32
- 5 Respostas
- 2613 Exibições
- Última mensagem por rafiusk

Dom Out 07, 2012 17:31
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas simples
por ninquewylia » Qui Abr 23, 2009 21:13
- 8 Respostas
- 7259 Exibições
- Última mensagem por rafagondi

Sex Abr 24, 2009 22:44
Álgebra Elementar
-
- duvidas de juros simples
por LAURELL3 » Ter Abr 12, 2011 18:44
- 3 Respostas
- 4563 Exibições
- Última mensagem por luizeduardo

Dom Abr 24, 2011 13:18
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Tente ler essa equação da seguinte forma:
. Tente ler essa equação da seguinte forma: 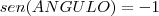 onde o
onde o 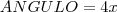 .
. , entre 0 e 90 graus, para os quais os ângulos iguais a
, entre 0 e 90 graus, para os quais os ângulos iguais a  tenham o seno igua a
tenham o seno igua a  .
.
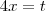 , portanto se
, portanto se 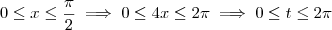 . Então teremos
. Então teremos 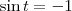 . Encontre t e volte para descobrir x.
. Encontre t e volte para descobrir x.

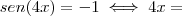 _____ graus
_____ graus 
 _____ / 4, logo
_____ / 4, logo