 por gustavowelp » Qua Jun 15, 2011 07:43
por gustavowelp » Qua Jun 15, 2011 07:43
Bom dia.
Estou tendo dificuldades em entender como resolver esta questão, que "parece", a princípio, ser fácil...
Um relógio analógico marca três horas e trinta minutos. Ao lado deste, outro relógio marca um fuso horário diferente: nove horas e trinta minutos.
Considere o ângulo agudo formado entre o ponteiro dos minutos e o ponteiro das horas, em cada um dos relógios, e assinale a alternativa CORRETA.
A resposta é:
O módulo da diferença entre os ângulos formados pelos ponteiros nos dois relógios é igual a 30º.
Não consegui ententer por que os ângulos não são iguais...
Obrigado!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por FilipeCaceres » Qua Jun 15, 2011 14:49
por FilipeCaceres » Qua Jun 15, 2011 14:49
Observe que quando for 3:30 o ponteiro das horas estará entre 3 e 4,ou seja o ângulo será (45-x), analogamente quando as horas for 9:30,o ponteiro das horas estará entre 9 e 10,ou seja o ângulo será (45+x).
Assim temos,
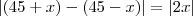
Onde x representa o ângulo formado pelo ponteiros dos minutos ao percorrer 30min.
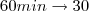
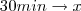
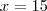
Portanto,
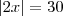
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- lógica com relógios
por jaquecox » Seg Mai 30, 2011 20:46
- 1 Respostas
- 4740 Exibições
- Última mensagem por Molina

Ter Mai 31, 2011 02:09
Lógica
-
- Ângulos e relógios
por Lovegood » Dom Set 29, 2013 09:50
- 0 Respostas
- 958 Exibições
- Última mensagem por Lovegood

Dom Set 29, 2013 09:50
Trigonometria
-
- Dois Problemas De P.A
por Guedes » Sex Out 08, 2010 13:44
- 5 Respostas
- 4531 Exibições
- Última mensagem por Augusto Evaristo

Sex Out 15, 2010 23:40
Progressões
-
- Interseção de dois planos
por bibs » Qui Ago 27, 2009 16:22
- 0 Respostas
- 5221 Exibições
- Última mensagem por bibs

Qui Ago 27, 2009 16:22
Geometria Analítica
-
- Interseção de dois planos
por bibs » Qui Ago 27, 2009 16:28
- 0 Respostas
- 2168 Exibições
- Última mensagem por bibs

Qui Ago 27, 2009 16:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


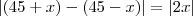
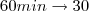
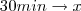
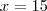
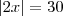

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.