 por vittor » Seg Fev 21, 2011 19:01
por vittor » Seg Fev 21, 2011 19:01
y = sen 2a
sen a .cos a
( Y igual seno de 2a, sobre seno de a, vezes cosseno de a )
_
Y = Cos 2a + Sen 2a
Como simplifica ?
Obrigado
-
vittor
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Fev 21, 2011 18:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 19:16
por Molina » Seg Fev 21, 2011 19:16
Boa tarde, Vitor.
Procure usar o LaTeX através do
Editor de Fórmulas para escrever expressões deste tipo.

Mas,
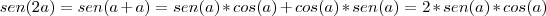
Assim:

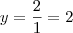

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Seno e cosseno de um arco trigonométrico, eu tentei resolver
por wesley_enrique » Dom Ago 08, 2010 19:38
- 6 Respostas
- 7718 Exibições
- Última mensagem por Pedro123

Seg Ago 09, 2010 18:59
Trigonometria
-
- arco duplo
por MERLAYNE » Qua Abr 04, 2012 19:52
- 1 Respostas
- 2502 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:57
Trigonometria
-
- [Arco Duplo]Cos(2a)
por Giudav » Sáb Set 15, 2012 12:48
- 2 Respostas
- 1936 Exibições
- Última mensagem por DanielFerreira

Sáb Set 15, 2012 22:38
Trigonometria
-
- [arco duplo] dúvida sobre questão
por marcelofacf » Qua Mai 15, 2013 18:03
- 0 Respostas
- 1254 Exibições
- Última mensagem por marcelofacf

Qua Mai 15, 2013 18:03
Trigonometria
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4661 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




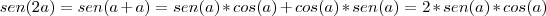

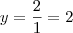


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)