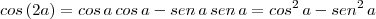por ElizabethS2 » Dom Nov 21, 2010 18:54
por ElizabethS2 » Dom Nov 21, 2010 18:54
Olá Gente estou com problemas em algumas questões de Identidades Trigonométricas.
a) (senx + tgx) . (cosx + cotgx) = (1 + senx) (1 + cosx)
b) sen²x + sen²y - sen2xsen²y + cos²xcos²y = 1
Por enquanto só tenho essas ! Ficaria muita grata se me ajudassem com essas questões. Muito obrigado e desde já agradeço!
-
ElizabethS2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 21, 2010 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Dom Nov 21, 2010 20:55
por VtinxD » Dom Nov 21, 2010 20:55
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por ElizabethS2 » Dom Nov 21, 2010 22:24
por ElizabethS2 » Dom Nov 21, 2010 22:24
VtinxD
A Equação é de acordo com a letra A . Muito obrigado de coração!
-
ElizabethS2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 21, 2010 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por ElizabethS2 » Ter Nov 23, 2010 17:11
por ElizabethS2 » Ter Nov 23, 2010 17:11
![[tex]cos^4x = sen^4x + cos2x \Leftrightarrow cos^4x -sen^4x = cos2x
a^2-b^2 = (a-b)(a+b)
(cos^2x)^2 - (sen^2x)^2 = (cos^2x -sen^2x)(cos^2x +sen^2x)
= cos^2x -sen^2x = cos2x [tex]cos^4x = sen^4x + cos2x \Leftrightarrow cos^4x -sen^4x = cos2x
a^2-b^2 = (a-b)(a+b)
(cos^2x)^2 - (sen^2x)^2 = (cos^2x -sen^2x)(cos^2x +sen^2x)
= cos^2x -sen^2x = cos2x](/latexrender/pictures/e58f739904436ff2f56b845c276bdb90.png)
[/tex]
Pessoal o professor passou essa questão. Entendi até a terceira parte mas na quarta não entendi de onde veio aquela expressão.
Poderiam me explicar o caminho que levou ficar desse jeito ?
-
ElizabethS2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 21, 2010 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Qua Nov 24, 2010 01:42
por VtinxD » Qua Nov 24, 2010 01:42
sen²(x)+cos²(x)=1
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por ElizabethS2 » Qua Nov 24, 2010 11:50
por ElizabethS2 » Qua Nov 24, 2010 11:50
Entendi como ficou. Já sabia que a relação fundamental valia 1! Mas não entendi pq cos^2x - sen^2x = cos2x
Pq ficou cos2x ???´isso é uma propriedade da trigonometria ?
-
ElizabethS2
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 21, 2010 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por caroltoscaON » Qua Nov 24, 2010 18:51
por caroltoscaON » Qua Nov 24, 2010 18:51
está certo.
-
caroltoscaON
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Nov 24, 2010 18:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


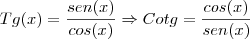
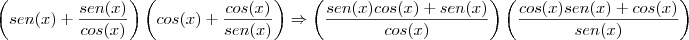
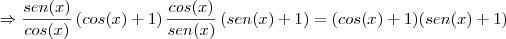
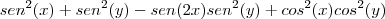
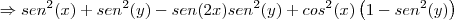
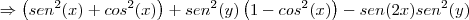
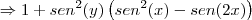

![[tex]cos^4x = sen^4x + cos2x \Leftrightarrow cos^4x -sen^4x = cos2x
a^2-b^2 = (a-b)(a+b)
(cos^2x)^2 - (sen^2x)^2 = (cos^2x -sen^2x)(cos^2x +sen^2x)
= cos^2x -sen^2x = cos2x [tex]cos^4x = sen^4x + cos2x \Leftrightarrow cos^4x -sen^4x = cos2x
a^2-b^2 = (a-b)(a+b)
(cos^2x)^2 - (sen^2x)^2 = (cos^2x -sen^2x)(cos^2x +sen^2x)
= cos^2x -sen^2x = cos2x](/latexrender/pictures/e58f739904436ff2f56b845c276bdb90.png) [/tex]
[/tex]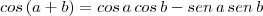
 :
: