-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480561 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 541475 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 505236 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 732665 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2174570 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por andersontricordiano » Qua Mar 23, 2011 17:19
por andersontricordiano » Qua Mar 23, 2011 17:19
Resolva a equação:
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )]](/latexrender/pictures/c1710d1f2f69dd4e3296358d5ae54f2c.png)
Detalhe a resposta é: -3 e 3
Obrigado quem resolver!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qua Mar 23, 2011 22:23
por Molina » Qua Mar 23, 2011 22:23
Boa noite, Anderson.
Você esqueceu do
sinal de igualdade.
Mas vou tentar ajudar mesmo assim, vamos por partes, ok? Sabemos que:
![\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}} = 10^{\frac{1}{1000}} \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}} = 10^{\frac{1}{1000}}](/latexrender/pictures/9ac99305fcc1c745e421a73a0b4ef44f.png)
Então:
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )]](/latexrender/pictures/c1710d1f2f69dd4e3296358d5ae54f2c.png)
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )]](/latexrender/pictures/944aa09b579bc861060e950fbee86ad9.png)
E que:
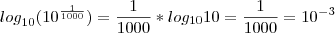
Então:
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )]](/latexrender/pictures/944aa09b579bc861060e950fbee86ad9.png)
![{3}^{{x}^{2}-18}+ {log}_{10} \left[ 10^{-3} \right] {3}^{{x}^{2}-18}+ {log}_{10} \left[ 10^{-3} \right]](/latexrender/pictures/0f56cc037c65957d0442a72452c295e0.png)

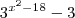
...
Agora é com você!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por jefferson0209 » Ter Set 22, 2015 18:40
por jefferson0209 » Ter Set 22, 2015 18:40
alguem me ajuda?
1)sendo log2=u e log3=v,determine:
a)log12
b)log15
2)calcula:
log 81+ log625-log100
.. 3 . . 5
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6218 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- resolva a equação logarítmica
por Debylow » Sex Nov 30, 2012 15:56
- 3 Respostas
- 1720 Exibições
- Última mensagem por young_jedi

Sex Nov 30, 2012 21:41
Logaritmos
-
- Resolva a seguinte equação:
por andersontricordiano » Sex Mar 28, 2014 23:38
- 1 Respostas
- 1688 Exibições
- Última mensagem por young_jedi

Sáb Mar 29, 2014 16:43
Análise Combinatória
-
- Resolva a seguinte equação logarítmica
por andersontricordiano » Qui Ago 04, 2011 18:32
- 4 Respostas
- 4482 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:41
Logaritmos
-
- Resolva a seguinte equação logarítmica
por andersontricordiano » Seg Ago 15, 2011 20:28
- 1 Respostas
- 1626 Exibições
- Última mensagem por Caradoc

Seg Ago 15, 2011 21:46
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )]](/latexrender/pictures/c1710d1f2f69dd4e3296358d5ae54f2c.png)

![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )]](/latexrender/pictures/c1710d1f2f69dd4e3296358d5ae54f2c.png)

![\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}} = 10^{\frac{1}{1000}} \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}} = 10^{\frac{1}{1000}}](/latexrender/pictures/9ac99305fcc1c745e421a73a0b4ef44f.png)
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}( \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} )]](/latexrender/pictures/c1710d1f2f69dd4e3296358d5ae54f2c.png)
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )]](/latexrender/pictures/944aa09b579bc861060e950fbee86ad9.png)
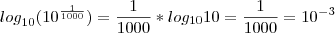
![{3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )] {3}^{{x}^{2}-18}+ {log}_{10} [ {log}_{10}(10^{\frac{1}{1000}} )]](/latexrender/pictures/944aa09b579bc861060e950fbee86ad9.png)
![{3}^{{x}^{2}-18}+ {log}_{10} \left[ 10^{-3} \right] {3}^{{x}^{2}-18}+ {log}_{10} \left[ 10^{-3} \right]](/latexrender/pictures/0f56cc037c65957d0442a72452c295e0.png)

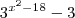




 .
.



