O enunciado diz o seguinte:
A magnitude aparente (m) e a magnitude absoluta (M) de uma estrela são grandezas utilizadas em astronomia para cular a distância (d) a que essa estrela se encontra da Terra. As três variáveis estão relacionadas pela fórmula
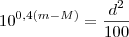
Prove que, para quaisquer m, M e d, se tem:
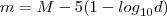
O livro tem uma proposta de resolução:
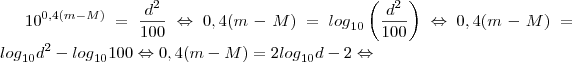
o que eu não entendo é como deste passo, eles passam para a expressão seguinte que é:
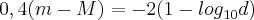
Porque é que
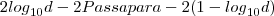 ???
???Estou dando em doida com estas expressões


 , imagine que você deseja colocar -2 em evidência.
, imagine que você deseja colocar -2 em evidência.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)