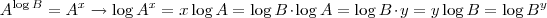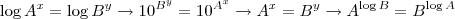Logaritmos.( Prove tal afirmação )
Eu tenho algumas questões desse tipo que não estou conseguindo resolver.
Se a , b e c são reais positivos com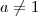 e
e 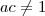 , prove que:
, prove que:
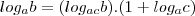
Se a , b e c são reais positivos com
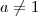 e
e 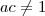 , prove que:
, prove que: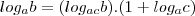
AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!
http://www.ajudamatematica.com/
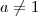 e
e 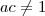 , prove que:
, prove que: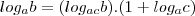
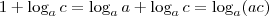
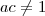 , caso contrário esse
, caso contrário esse  seria zero e o produto seria zero. Vamos ao produto:
seria zero e o produto seria zero. Vamos ao produto: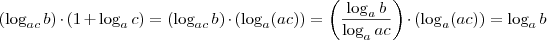
Fantini escreveu:Daniel, vou sair do segundo lado e chegar no primeiro. Primeiro, note que:
O que mostra a necessidade de, caso contrário esse
seria zero e o produto seria zero. Vamos ao produto:
Provado.
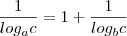
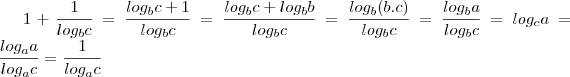

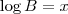 e
e 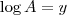 . Então
. Então