Danilo Dias Vilela escreveu:Gostaria de ajuda na seguinte equação:

Desde já agradeço.
Boa tarde, Danilo.
A dica que eu posso dar é você fazer
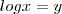
e resolver então:
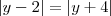
Como está em módulo dos dois lados, você pode fazer duas equações: uma supondo que em ambos os lados há o mesmo sinal e outra supondo que um dos lados é positivo e o outro lado é negativo.
Você verá que considerando ambos os lados com o mesmo sinal ele não terá resposta.
Então o que você precisará calcular é:
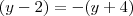
(mantive o sinal do lado esquerdo e alterei o lado direito).
Depois que encontrar y volte na condição inicial de

e descubra x.





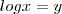 e resolver então:
e resolver então: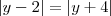
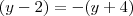
 e descubra x.
e descubra x.
