2 Exercícios de Log.

[julianows]

Boa Noite estou com algumas dificuldades em dois exercícios.

1°- O valor de X que satisfaz a equação é

a)-1
b)0
c)1
d)2 <---
e)3

este seria o primeiro
eu consegui resolver mas me tranquei em uma parte, devo ter errado algo

Aqui está minha tentativa




2°- Numa cidade do interior, um médico pediatra, após registrar por vários anos o crescimento de pacientes com idades entre 1 e 12 anos chegou a formula que indica a altura média das crianças.



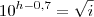
onde h respresenta a altura em metros e i, a idade em anos. Assim, supondo que o log 3 = 0,48, a altura média de uam criança de 9 anos, em metros será

a)1,15
b)1,16
c)1,17
d)1,18 <---
e)1,19

Bom seria isso, se alguem estiver disposto a me tirar estas dúvidas ficarei muito grato.

[Elcioschin]

No primeiro vc parou no meio do caminho:

x + 2 = x²

x² - x - 2 = 0 ----> Equação do 2º grau ----> Bhaskara ----> Raízes ----> x = 2 ou x = -1

A raiz x = - 1 não serve pois x é uma base de log e a base é sempre maior do que zero ---> x > 0

Solução ----> x = 2

Quanto ao segundo:

10^(h - 0,7) = V(i) ----> 10^(h - 0,7) = i^(1/2) ----> Aplicando log na base 10:

log[10]{10^(h - 0,7)} = log[10]{i^(1/2)}

(h - 0,7)*log[10](10) = (1/2)*log[10](i) ----> i = 9 = 3²

(h - 0,7)*log[10](10) = (1/2)*log[10](3²)

(h - 0,7)*1 = (1/2)*2*log[10](3)

h - 0,7 = log[10](3) ----> h - 0,7 = 0,48 ----> h = 1,18

Por favor, coloque apenas 1 questão por tópico, daqui em diante.

[julianows]

Elcioschin muito orbigado e desculpa por postar mais de uma questão ... não vai acontecer mais.