 por lucassouza » Qua Nov 12, 2014 17:47
por lucassouza » Qua Nov 12, 2014 17:47
Adauto, agradeço pela ajuda que vc tem dado para mim e para todos nas resoluções de exercícios. Estou enviando uma imagem com outra dúvida que surgiu enquanto fazia outras atividades. Agradeço desde já!
- Anexos
-

- Mudar Logaritmos de membro é válido?
-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por adauto martins » Qua Nov 12, 2014 20:07
por adauto martins » Qua Nov 12, 2014 20:07
caro lucas,
sim com certeza,pois a base dos logaritmos sao a mesma...ai agora vc usa a propriedade

...entao teremos:
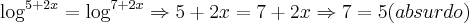
...logo nao existe soluçao para a expressao dada...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por lucassouza » Qua Nov 12, 2014 22:14
por lucassouza » Qua Nov 12, 2014 22:14
adauto martins escreveu:caro lucas,
sim com certeza,pois a base dos logaritmos sao a mesma...ai agora vc usa a propriedade

...entao teremos:
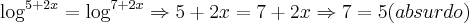
...logo nao existe soluçao para a expressao dada...
xD, vlw. Entendi, então somente quando possuírem bases iguais que essa mudança de membro é válida. Mas não precisava resolver não xD, mas obrigado!
-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1853 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2741 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5273 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2283 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ...entao teremos:
...entao teremos: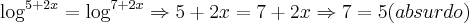 ...logo nao existe soluçao para a expressao dada...
...logo nao existe soluçao para a expressao dada...
...entao teremos:
...logo nao existe soluçao para a expressao dada...
