 por thamysoares » Sex Nov 16, 2012 11:27
por thamysoares » Sex Nov 16, 2012 11:27
Resolva o sistema de equações nas incógnitas x e y.
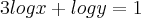
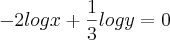
Me ajudem? Não sei nem logaritmo direito quanto mais logaritmo em um sistema. Por favor.
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 16, 2012 11:55
por e8group » Sex Nov 16, 2012 11:55
isole ,
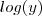
ou
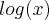
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
EX:
Somando
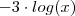
, na primeira equação :

Agora substitua na segunda equação .
Consegue terminar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thamysoares » Sex Nov 16, 2012 13:49
por thamysoares » Sex Nov 16, 2012 13:49
santhiago escreveu:isole ,
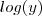
ou
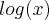
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
EX:
Somando
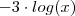
, na primeira equação :

Agora substitua na segunda equação .
Consegue terminar ?
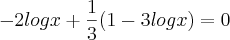
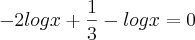
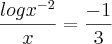
E então?
Eu não sei como se faz =[
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 16, 2012 16:31
por e8group » Sex Nov 16, 2012 16:31
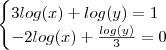
.
No tópico , acima , vimos que
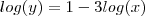
. Susbstituindo na segunda equação ,
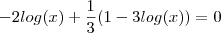
.
Multiplicando toda equação por

,
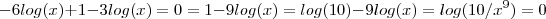
Sabemos que
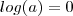
quando

Com isso ,
![log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10} log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10}](/latexrender/pictures/793a82e214f7f9044b6b1ed66187a874.png)
.
Para resolver para

, isole
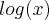
da relação
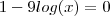
, susbstitua em
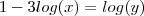
. Faça a mesma análise e resolva p/ y .
Por favor revise seus cálculos .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thamysoares » Sex Nov 16, 2012 18:17
por thamysoares » Sex Nov 16, 2012 18:17
santhiago escreveu: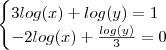
.
No tópico , acima , vimos que
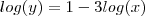
. Susbstituindo na segunda equação ,
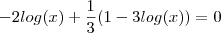
.
Multiplicando toda equação por

,
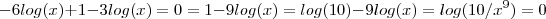
Sabemos que
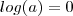
quando

Com isso ,
![log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10} log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10}](/latexrender/pictures/793a82e214f7f9044b6b1ed66187a874.png)
.
Para resolver para

, isole
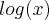
da relação
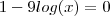
, susbstitua em
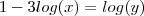
. Faça a mesma análise e resolva p/ y .
Por favor revise seus cálculos .
Bom, eu tentei fazer como você disse. Veja se está correto, por favor:
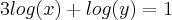
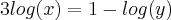
Então eu multipliquei por -2 pra substituir na outra equação, que eu multipliquei por -3(nem sei se pode fazer isso). Assim:
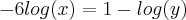
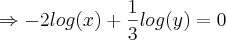
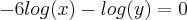
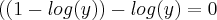
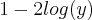
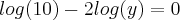
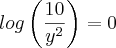
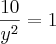

![y=\sqrt[]{10} y=\sqrt[]{10}](/latexrender/pictures/d0222f9916cde01009d3db653d22c32a.png)
E então?
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 16, 2012 19:31
por e8group » Sex Nov 16, 2012 19:31
Cuidado ! você cometeu um erro grave que estar alterando o resultado .
Veja o certo ,
Multiplicando
ambos lados da igualdade por - 2 .
Vamos obter ,
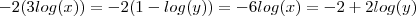
Perceba que , basta multiplicar pelo seu inverso , que vamos desfazer a operação anterior , isto é , multiplique toda toda equação por

que voltará para a equação original .
Observe o seu desenvolvimento e faça uma comparação .
Mas , como já temos
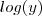
em função de
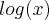
, lembrando
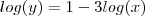
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
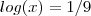
( Observe minha 2ª resposta ao tópico ) .
Sendo assim ,
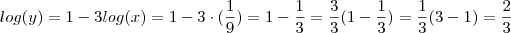
.
Daí ,
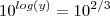
e
Portanto ,
![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)
Qualquer coisa comente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thamysoares » Sex Nov 16, 2012 19:56
por thamysoares » Sex Nov 16, 2012 19:56
santhiago escreveu:Cuidado ! você cometeu um erro grave que estar alterando o resultado .
Veja o certo ,
Multiplicando
ambos lados da igualdade por - 2 .
Vamos obter ,
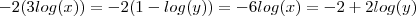
Perceba que , basta multiplicar pelo seu inverso , que vamos desfazer a operação anterior , isto é , multiplique toda toda equação por

que voltará para a equação original .
Observe o seu desenvolvimento e faça uma comparação .
Mas , como já temos
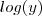
em função de
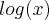
, lembrando
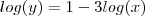
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
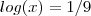
( Observe minha 2ª resposta ao tópico ) .
Sendo assim ,
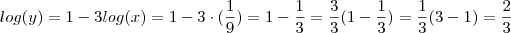
.
Daí ,
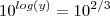
e
Portanto ,
![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)
Qualquer coisa comente .
Muitíssimo obrigada =D
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5040 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6669 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 3361 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- LOGARITMOS
por DESESPERADA » Qua Dez 30, 2009 13:25
- 2 Respostas
- 3130 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:37
Matemática Financeira
-
- Logaritmos
por cristina » Qua Jun 02, 2010 10:07
- 1 Respostas
- 2422 Exibições
- Última mensagem por Cleyson007

Qua Jun 02, 2010 13:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
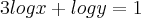
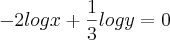

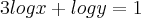
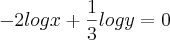

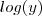 ou
ou 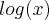 , depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita . 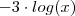 , na primeira equação :
, na primeira equação : 

ou
, depois substitua na segunda equação . Resolva para a variável que restar e depois volte na primeira equação e resolva p/ a outra incógnita .
, na primeira equação :

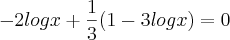
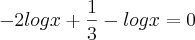
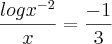

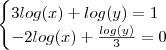 .
. 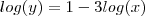 . Susbstituindo na segunda equação ,
. Susbstituindo na segunda equação , 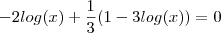 .
.  ,
, 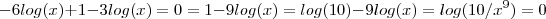
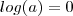 quando
quando 
![log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10} log(10/x^9) = 0 \iff 10/x^9 = 1 \iff 10 = x^9 \iff x = 10^{1/9} = \sqrt[9]{10}](/latexrender/pictures/793a82e214f7f9044b6b1ed66187a874.png) .
.  , isole
, isole 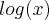 da relação
da relação 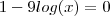 , susbstitua em
, susbstitua em 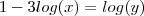 . Faça a mesma análise e resolva p/ y .
. Faça a mesma análise e resolva p/ y . 
.
. Susbstituindo na segunda equação ,
.
,
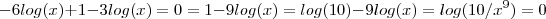
quando

.
, isole
da relação
, susbstitua em
. Faça a mesma análise e resolva p/ y .
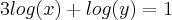
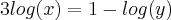
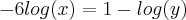
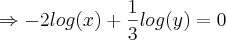
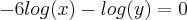
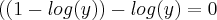
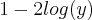
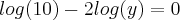
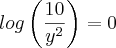
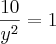

![y=\sqrt[]{10} y=\sqrt[]{10}](/latexrender/pictures/d0222f9916cde01009d3db653d22c32a.png)

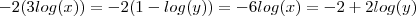
 que voltará para a equação original .
que voltará para a equação original . 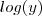 em função de
em função de 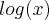 , lembrando
, lembrando 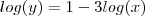 ( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos 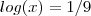 ( Observe minha 2ª resposta ao tópico ) .
( Observe minha 2ª resposta ao tópico ) . 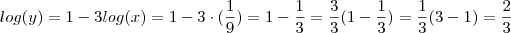 .
. 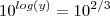
![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)

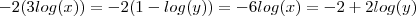
que voltará para a equação original .
em função de
, lembrando
( Observe minha 1ª resposta ao tópico ) e ressaltando também já temos
( Observe minha 2ª resposta ao tópico ) .
.
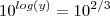
![y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100} y = 10^{2/3} = (10^2 )^{1/3} = \sqrt[3]{10^2} = \sqrt[3]{100}](/latexrender/pictures/c93da929a12837ef7a7181326e2a8f81.png)
![S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \} S = \left\{ (\sqrt[9]{10} , \sqrt[3]{100} ) \right \}](/latexrender/pictures/611b3c1766977b3185027f01871f77e9.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.