 por moyses » Dom Dez 11, 2011 22:37
por moyses » Dom Dez 11, 2011 22:37
Oi pessoal beleza? bom nesse ferias eu estava estudando logaritmos e eu me deparei com um exerecicio interresante e que me chamou a atençao, pois vamos ao que interessa nao e ? bem ai esta: Determine
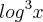
e
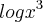
, sabendo que
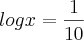
? a minha duvida ´´e como resolver esse daqui
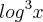
porque o primeiro ta facil eu ja sei, mais e esse da ai com o espoente no log endes? me ajudem ai fazendo favor ? desde de ja grato!

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Dez 11, 2011 23:53
por MarceloFantini » Dom Dez 11, 2011 23:53
Imagino que
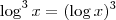
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por moyses » Seg Dez 12, 2011 11:57
por moyses » Seg Dez 12, 2011 11:57
ahh é igual aquele propriedade quando eu pego multiplico por exemplo
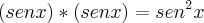
então
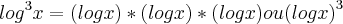
? é só isso?

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por MarceloFantini » Seg Dez 12, 2011 15:53
por MarceloFantini » Seg Dez 12, 2011 15:53
É só isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por moyses » Qui Dez 15, 2011 12:05
por moyses » Qui Dez 15, 2011 12:05
valeww obrigado pela ajuda!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5040 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- Dúvida com logaritmos
por AntonioG » Qui Dez 09, 2010 10:46
- 1 Respostas
- 1686 Exibições
- Última mensagem por vyhonda

Qui Dez 09, 2010 12:13
Logaritmos
-
- [Logaritmos] Dúvida
por fff » Sáb Dez 21, 2013 11:40
- 4 Respostas
- 2246 Exibições
- Última mensagem por fff

Sáb Dez 21, 2013 18:26
Logaritmos
-
- [Logaritmos] Dúvida em Inequação com ln
por PauloP » Ter Fev 09, 2016 15:41
- 1 Respostas
- 3347 Exibições
- Última mensagem por petras

Sex Dez 02, 2016 23:56
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6669 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
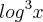 e
e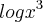 , sabendo que
, sabendo que 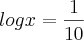 ? a minha duvida ´´e como resolver esse daqui
? a minha duvida ´´e como resolver esse daqui 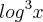 porque o primeiro ta facil eu ja sei, mais e esse da ai com o espoente no log endes? me ajudem ai fazendo favor ? desde de ja grato!
porque o primeiro ta facil eu ja sei, mais e esse da ai com o espoente no log endes? me ajudem ai fazendo favor ? desde de ja grato! 

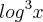 e
e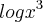 , sabendo que
, sabendo que 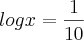 ? a minha duvida ´´e como resolver esse daqui
? a minha duvida ´´e como resolver esse daqui 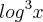 porque o primeiro ta facil eu ja sei, mais e esse da ai com o espoente no log endes? me ajudem ai fazendo favor ? desde de ja grato!
porque o primeiro ta facil eu ja sei, mais e esse da ai com o espoente no log endes? me ajudem ai fazendo favor ? desde de ja grato! 


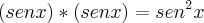 então
então 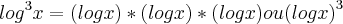 ? é só isso?
? é só isso? 



