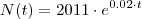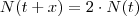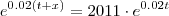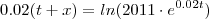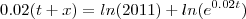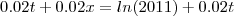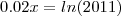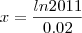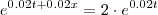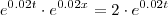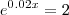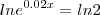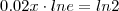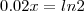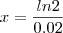por joaofonseca » Ter Jun 21, 2011 13:39
por joaofonseca » Ter Jun 21, 2011 13:39
Seja a função:
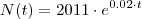
Em que
N é a quantidade de plantas após
t dias.
Determine
x de forma que para qualquer
t se verifique:
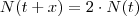
A interpretação deste problema é: passados
x dias do dia
t tem-se o dobro das plantas.
Eu tentei:

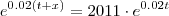
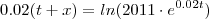
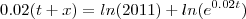
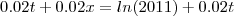
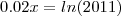
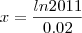
No entanto o resultado a que eu cheguei não coincide com o gabarito (34,7) nem com a representação gráfica.
Onde errei?
Obrigado pela ajuda
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Ter Jun 21, 2011 14:45
por Molina » Ter Jun 21, 2011 14:45
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Claudin » Ter Jun 21, 2011 15:11
por Claudin » Ter Jun 21, 2011 15:11
O erro foi em retirar o 2011 somente do 1º membro.
E uma observação seria quando for aplicar o logaritmo neperiano, você foi bem direto utilizando propriedade de logaritmos no 1º membro, tendo como resultado os expoentes, tente desenvolver como o Molina passo a passo, irá evitar erros e facilita o entendimento dos demais usuários do fórum.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5040 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6669 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- Exponenciais
por Souo » Ter Jun 30, 2015 01:42
- 3 Respostas
- 2705 Exibições
- Última mensagem por nakagumahissao

Sex Jul 03, 2015 21:24
Logaritmos
-
- Exponenciais
por Souo » Sáb Jun 20, 2015 14:45
- 1 Respostas
- 1764 Exibições
- Última mensagem por Cleyson007

Dom Jun 21, 2015 09:20
Logaritmos
-
- Exponenciais
por Souo » Qui Jun 18, 2015 19:09
- 1 Respostas
- 1673 Exibições
- Última mensagem por nakagumahissao

Sex Jun 19, 2015 18:50
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.