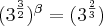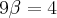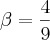por umaiafilho » Sáb Mai 21, 2011 19:18
por umaiafilho » Sáb Mai 21, 2011 19:18
Usando a definição de logaritimo para recair numa equação exponencial:
a)
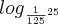
resolução
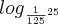
= y >> 25=
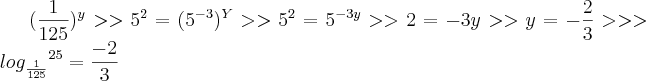
problema 1
![{log}_{\sqrt[]{2}}{}^{0,125} {log}_{\sqrt[]{2}}{}^{0,125}](/latexrender/pictures/ba702f74880312017314d990ff6cba46.png)
problema 2
![{log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}} {log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}}](/latexrender/pictures/b45ea78a07b4153bf97a2cc2e462ca18.png)
agradeço quem puder me ajudar!
-
umaiafilho
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qui Mai 12, 2011 20:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CONTABEIS
- Andamento: cursando
 por DanielFerreira » Dom Mar 04, 2012 10:50
por DanielFerreira » Dom Mar 04, 2012 10:50
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Mar 04, 2012 11:00
por DanielFerreira » Dom Mar 04, 2012 11:00
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1853 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2741 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5272 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2283 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
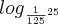
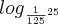 = y >> 25=
= y >> 25=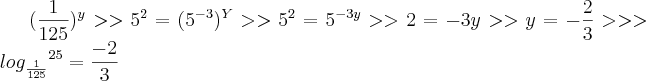
![{log}_{\sqrt[]{2}}{}^{0,125} {log}_{\sqrt[]{2}}{}^{0,125}](/latexrender/pictures/ba702f74880312017314d990ff6cba46.png)
![{log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}} {log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}}](/latexrender/pictures/b45ea78a07b4153bf97a2cc2e462ca18.png)

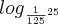
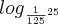 = y >> 25=
= y >> 25=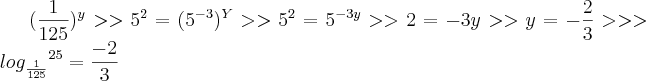
![{log}_{\sqrt[]{2}}{}^{0,125} {log}_{\sqrt[]{2}}{}^{0,125}](/latexrender/pictures/ba702f74880312017314d990ff6cba46.png)
![{log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}} {log}_{\sqrt[]{27}}{}^{\sqrt[3]{9}}](/latexrender/pictures/b45ea78a07b4153bf97a2cc2e462ca18.png)

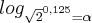
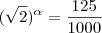
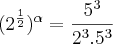
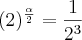
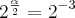


![log_\sqrt{27}^{\sqrt[3]{9}} = \beta log_\sqrt{27}^{\sqrt[3]{9}} = \beta](/latexrender/pictures/9240bbbca7d3111973a3d51d2b4c7823.png)
![(\sqrt{27})^\beta = \sqrt[3]{9} (\sqrt{27})^\beta = \sqrt[3]{9}](/latexrender/pictures/f058f7b9fbd49e80ba0597d0b7c166a4.png)