por Elcioschin » Seg Abr 04, 2011 20:02
Desenvolvendo os expoentes:
a) 5 + log2(3) = log2(2^5) + log2(3) = log2(32) + log2(3) = log2(96)
b) log2(7)*log3(2) = log3(7)
m = 2^log2(96) + 3^log3(7) ----> m = 96 + 7 ----> m = 103
-
Elcioschin
- Colaborador Voluntário
-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcule o valor de m no seguinte exercício
por andersontricordiano » Seg Abr 04, 2011 14:59
- 1 Respostas
- 1383 Exibições
- Última mensagem por Elcioschin
Seg Abr 04, 2011 20:05
Logaritmos
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3710 Exibições
- Última mensagem por adauto martins
Qui Fev 19, 2015 15:41
Trigonometria
-
- Valor de a na seguinte matriz
por fmach » Ter Jan 25, 2011 17:03
- 0 Respostas
- 1482 Exibições
- Última mensagem por fmach
Ter Jan 25, 2011 17:03
Matrizes e Determinantes
-
- Como calcular porcentagem do seguinte valor:?
por icaro » Ter Jan 23, 2018 12:23
- 1 Respostas
- 8366 Exibições
- Última mensagem por DanielFerreira
Qui Jan 25, 2018 11:31
Aritmética
-
- (calculo III) resolva o seguinte problema de valor inicial
por liviabgomes » Qui Dez 01, 2011 14:59
- 4 Respostas
- 2188 Exibições
- Última mensagem por liviabgomes
Seg Dez 05, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30
Então, o exercicio pede para encontrar
.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:
Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):
Somando a primeira e a segunda equação:
Finalmente:
Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
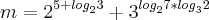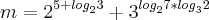, qual é o valor de m?