a) ( ) Interceptam-se em dois pontos.
b) ( ) Não se interceptam.
c) ( ) Interceptam-se em um único ponto de abscissa negativa.
d) ( ) Interceptam-se em um único ponto de abscissa positiva.
e) ( ) Interceptam-se em um único ponto de ordenada negativa.
Bom, eu igualei f(x) com g(x), porém estou chegando a dois valores para x (uma vez que obtive a seguinte equação de segundo grau:
 ). Aí agora não me lembro o que devo fazer: isso quer dizer que as duas funções acima se interceptam em dois pontos ou quer dizer que elas não se interceptam?
). Aí agora não me lembro o que devo fazer: isso quer dizer que as duas funções acima se interceptam em dois pontos ou quer dizer que elas não se interceptam?


![x = (1 + \sqrt[]{5}) / 2 x = (1 + \sqrt[]{5}) / 2](/latexrender/pictures/b39be8448a1b74caf76e988e9975a495.png) ou
ou ![x = (1 - \sqrt[]{5}) / 2 x = (1 - \sqrt[]{5}) / 2](/latexrender/pictures/5df5dc6cf35d63fd6a15b7e9bf7f418f.png) . Dessa forma como eu faço pra ver se estes valores satisfazem a equação? Ou isso já quer dizer que a equação tem duas soluções e portanto as funções se interceptam em dois pontos?
. Dessa forma como eu faço pra ver se estes valores satisfazem a equação? Ou isso já quer dizer que a equação tem duas soluções e portanto as funções se interceptam em dois pontos? que você encontrou tanto em
que você encontrou tanto em  com em
com em  e desenvolver - ambos os resultados devem ser iguais.
e desenvolver - ambos os resultados devem ser iguais.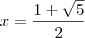 :
: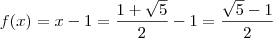
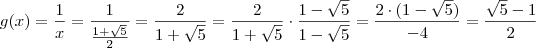
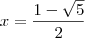


 , avisa que eu resolvo.
, avisa que eu resolvo.

