 por Jhenrique » Qui Set 13, 2012 02:30
por Jhenrique » Qui Set 13, 2012 02:30
Saudações caros estudantes!
Vou começar definindo 2 acepções para o termo função:
1) no sentido geral: conjunto de operações executadas por algo ou alguém.
2) no sentido matemático: uma grandeza y variando por causa da variação duma grandeza x
Pois bem, é certo afirmar que a Integração ou a Derivação duma função genérica f(x) é uma função no 2º sentido acima citado por mim, o matemático?
Creio que sim, porque:
seja y uma função f(x) qualquer
der(y) = y'
int(y) = Y
aplicamos a derivada e a integral numa função genérica como aplicamos a função seno e cosseno num ângulo qualquer... não é verdade!?
PS.: sendo y?¹ uma função inversa genérica, a melhor notação (sem colchetes) para denotar a sua derivada seria: y?¹' ou y'?¹ ?
Obg,
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Qui Set 13, 2012 10:12
por MarceloFantini » Qui Set 13, 2012 10:12
Uma função entre dois conjuntos é uma regra que associa cada elemento do conjunto domínio a um elemento do contradomínio. Eu pelo menos acredito que esta idéia de que uma função é uma grandeza variando devido á variação de outra limita seu pensamento, pois existem funções das mais diversas formas e isto atrapalharia sua interpretação.
Sobre sua pergunta, sim: derivadas e integrais de uma função são funções. Muitas vezes são tomadas inclusive como o ponto de partida delas: uma das definições de logaritmo é
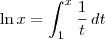
, para tomar um exemplo simples.
aplicamos a derivada e a integral numa função genérica como aplicamos a função seno e cosseno num ângulo qualquer... não é verdade!?
Não tão genérica assim. Aplicamos derivadas em funções que sejam deriváveis e integrais em funções que sejam contínuas. São classes de funções bem restritas.
Sobre a notação, acredito que seja
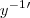
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Diferenciação Logarítmica
por Man Utd » Dom Mai 26, 2013 16:02
- 3 Respostas
- 2362 Exibições
- Última mensagem por e8group

Dom Mai 26, 2013 19:00
Cálculo: Limites, Derivadas e Integrais
-
- integraçao de potencia e produtos de funçoes trigonometricas
por menino de ouro » Dom Nov 04, 2012 19:46
- 3 Respostas
- 1200 Exibições
- Última mensagem por MarceloFantini

Seg Nov 05, 2012 10:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5799 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limites de Integração] Como achar os limites de integração?
por Miine_J » Sáb Nov 10, 2018 03:13
- 2 Respostas
- 19512 Exibições
- Última mensagem por Miine_J

Dom Nov 11, 2018 08:17
Cálculo: Limites, Derivadas e Integrais
-
- Integração
por Cleyson007 » Seg Out 29, 2012 19:33
- 6 Respostas
- 4107 Exibições
- Última mensagem por Cleyson007

Ter Out 30, 2012 10:31
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


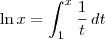 , para tomar um exemplo simples.
, para tomar um exemplo simples.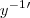 .
.






