 por angelmix » Dom Jul 22, 2012 16:53
por angelmix » Dom Jul 22, 2012 16:53
Alguém pode me ajudar neste exercício?
Qual é a imagem de f(x)=1/raiz quadrada de x²-1? ela é injetora ou sobrejetora?
-
angelmix
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Out 19, 2011 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por fraol » Dom Jul 22, 2012 20:50
por fraol » Dom Jul 22, 2012 20:50
Boa noite,
O domínio dessa função é
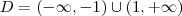
.
A imagem dessa função é
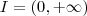
.
A função
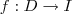
é sobrejetora mas não é injetora pois, por exemplo,
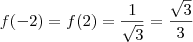
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Ter Jul 24, 2012 19:09
por fraol » Ter Jul 24, 2012 19:09
Contudo, cabe um comentário: se a dita função for
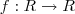
então ela não será sobrejetora.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Qua Jul 25, 2012 05:27
por MarceloFantini » Qua Jul 25, 2012 05:27
O maior domínio que ela pode ter é
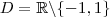
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Sex Jul 27, 2012 20:53
por fraol » Sex Jul 27, 2012 20:53
Boa noite,
O domínio de
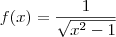
é
![D = \mathbb{R} \backslash [ -1, 1] D = \mathbb{R} \backslash [ -1, 1]](/latexrender/pictures/8b76f21dd20f2b4a32b77849a5d9e32d.png)
.
Os valores entre -1 e 1 também não estão no domínio.
MarceloFantini Por que você fala
O maior domínio ...
?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Sex Jul 27, 2012 20:57
por MarceloFantini » Sex Jul 27, 2012 20:57
Porque o domínio é algo que deve ser especificado sempre que é dada a função, e não algo que se "calcula". Poderíamos defini-la no intervalo
![[3,5] [3,5]](/latexrender/pictures/f53af11412591f12d4a404e2de96a921.png)
, por exemplo. É um domínio perfeitamente válido, entretanto não é o maior domínio possível.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Sex Jul 27, 2012 21:02
por fraol » Sex Jul 27, 2012 21:02
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4199 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3141 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3392 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2998 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


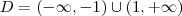 .
.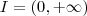 .
.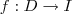 é sobrejetora mas não é injetora pois, por exemplo,
é sobrejetora mas não é injetora pois, por exemplo, 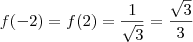 .
.
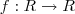 então ela não será sobrejetora.
então ela não será sobrejetora.

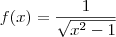 é
é ![D = \mathbb{R} \backslash [ -1, 1] D = \mathbb{R} \backslash [ -1, 1]](/latexrender/pictures/8b76f21dd20f2b4a32b77849a5d9e32d.png) .
.
![[3,5] [3,5]](/latexrender/pictures/f53af11412591f12d4a404e2de96a921.png) , por exemplo. É um domínio perfeitamente válido, entretanto não é o maior domínio possível.
, por exemplo. É um domínio perfeitamente válido, entretanto não é o maior domínio possível.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.