Gostaria de entender melhor a o domínio e a imagem da função abaixo.
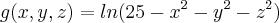
Se a função tivesse somente 2 variáveis (x,y em função de z), o domínio estaria no plano x,y e a imagem correspondente em z.
Mas essa função tem 3 variávies, não consigo entender nem como ficaria isso graficamente.
Grata


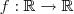 , temos uma curva em
, temos uma curva em 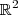 . Quando temos uma função
. Quando temos uma função 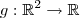 , temos uma superfície em
, temos uma superfície em 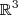 . Qual seria sua conclusão quando temos uma função
. Qual seria sua conclusão quando temos uma função 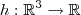 ?
?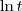 requer que
requer que 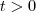 , também lembre-se que logaritmo é um
, também lembre-se que logaritmo é um 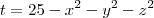 , nossa condição torna-se
, nossa condição torna-se 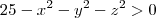 . O que podemos dizer então?
. O que podemos dizer então?

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)