 por fenixxx » Ter Fev 28, 2012 21:28
por fenixxx » Ter Fev 28, 2012 21:28
a) Determine a fração


Q que resolve a equação

. Dica: Faça
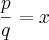
. (Observação: A resposta pode ser expressa em forma de fração irredutível ou por representação decimal, mas, a solução ficará errada se usar aproximação.)
b) Resolva a equação para a incógnita x,
ax+
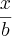
- 5 - x = 1,1
onde

e
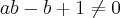
. Em seguida, faça uma análise do que acontece com a solução da equação, se ab - b + 1 = 0. Ela existe ou não?
c) O valor da área de um quadrado, segundo uma determinada unidade de medida u, é 9
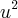
. Determine a medida do perímetro do quadrado numa nova unidade
de medida u’ que é um quinto da unidade de medida u.
-
fenixxx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Fev 28, 2012 21:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por MarceloFantini » Ter Fev 28, 2012 21:58
por MarceloFantini » Ter Fev 28, 2012 21:58
Fenix, bem-vindo ao fórum. Primeiramente, quero lembrar que o objetivo do fórum não é resolver listas de exercícios. Segundo, poste-os separadamente, e cada com mostrando suas tentativas. Por último, vale perceber que não são "frações" de equações, mas sim equações com frações.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fenixxx » Qua Fev 29, 2012 17:08
por fenixxx » Qua Fev 29, 2012 17:08
hm ... ta
caindo fora do forun então, vlw !!!!
-
fenixxx
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Fev 28, 2012 21:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar as equações
por [icaro] » Sáb Mar 26, 2011 15:25
- 1 Respostas
- 1271 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 26, 2011 17:03
Geometria Analítica
-
- Equações com frações com duas incognitas
por Jean Cigari » Qui Jun 23, 2011 12:39
- 2 Respostas
- 5240 Exibições
- Última mensagem por Molina

Qui Jun 23, 2011 15:55
Cálculo: Limites, Derivadas e Integrais
-
- Como determinar o conjunto solução das seguintes equações?
por gahzurc » Qui Abr 24, 2014 17:21
- 1 Respostas
- 5805 Exibições
- Última mensagem por fff

Sex Abr 25, 2014 10:47
Equações
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3155 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3432 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 Q que resolve a equação
Q que resolve a equação  . Dica: Faça
. Dica: Faça 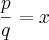 . (Observação: A resposta pode ser expressa em forma de fração irredutível ou por representação decimal, mas, a solução ficará errada se usar aproximação.)
. (Observação: A resposta pode ser expressa em forma de fração irredutível ou por representação decimal, mas, a solução ficará errada se usar aproximação.) 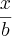 - 5 - x = 1,1
- 5 - x = 1,1 e
e 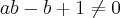 . Em seguida, faça uma análise do que acontece com a solução da equação, se ab - b + 1 = 0. Ela existe ou não?
. Em seguida, faça uma análise do que acontece com a solução da equação, se ab - b + 1 = 0. Ela existe ou não? 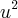 . Determine a medida do perímetro do quadrado numa nova unidade
. Determine a medida do perímetro do quadrado numa nova unidade



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
