Apesar de saber como se resolve essa questão eu não entendi onde realmente foi calculado a inversa de sen (1/3)
Pois o método de resolução é
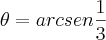, logo 
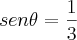depois toma-se um triângulo de cateto oposto igual a 1 e hipotenusa igual a 3 e acha-se o outro lado e a partir daí encontra-se a tangente. Quanto a resolução deste problema eu não tenho dúvida, eu só não vi onde a inversa foi calculada visto que ela deveria vir em radianos.Obs: essa questão é um exercício resolvido do assunto "Funções inversas trigonométricas", talvez se não estivesse nesse assunto eu nem teria tido esta dúvida.
Agradeço desde já a quem me ajudar a entender!
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
A DÚVIDA JÁ FOI ESCLARECIDA
**************************************************************************************************************************************************
CASO QUEIRAM COLOCAR ALGUM COMENTÁRIO, AGRADEÇO!!
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.