[Funções] Gráfico e Função

[lucsrlx]

Olá pessoal, gostaria de saber se voces podem me ajudar com o exercício abaixo, pois não faço ideia de onde começar, já que o gráfico não fornece raízes, mas apenas pontos, e o enunciado também não da a lei de f(x), nao faço ideia por onde começo, grato

http://hospedarimagem.com.br/?v=PfBMw.png

[LuizAquino]

Olá pessoal, gostaria de saber se voces podem me ajudar com o exercício abaixo, pois não faço ideia de onde começar, já que o gráfico não fornece raízes, mas apenas pontos, e o enunciado também não da a lei de f(x), nao faço ideia por onde começo, grato

http://hospedarimagem.com.br/?v=PfBMw.png

Por favor, por questão de organização do fórum, escreva aqui todo o texto do exercício, enviando como imagem apenas o que for necessário.

Aproveito para frisar que enviar o texto do exercício como uma imagem prejudica o sistema de busca do fórum.

[lucsrlx]

Olá pessoal, gostaria de saber se voces podem me ajudar com o exercício abaixo, pois não faço ideia de onde começar, já que o gráfico não fornece raízes, mas apenas pontos, e o enunciado também não da a lei de f(x), nao faço ideia por onde começo, grato

http://hospedarimagem.com.br/?v=PfBMw.png

Por favor, por questão de organização do fórum, escreva aqui todo o texto do exercício, enviando como imagem apenas o que for necessário.

Aproveito para frisar que enviar o texto do exercício como uma imagem prejudica o sistema de busca do fórum.

Olá, peço desculpas, não sabia deste procedimento, apenas coloquei a imagem pelo fato da existência do gráfico, mas segue o texto:

"A figura indica o grafico da função contínua f, de domínio [-12, 16] e imagem [-5, 16].

De acordo com o gráfico, o número de soluções da equação f(f(x)) = 5 é

(A) 3 / (B) 4 / (C) 5 / (D) 6 / (E) 7"

[LuizAquino]

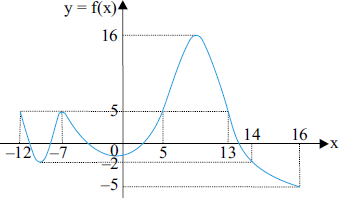
"A figura indica o grafico da função contínua f, de domínio [-12, 16] e imagem [-5, 16].

De acordo com o gráfico, o número de soluções da equação f(f(x)) = 5 é

(A) 3 / (B) 4 / (C) 5 / (D) 6 / (E) 7"

Eis a figura:

figura.png (10.41 KiB) Exibido 11825 vezes

Da análise do gráfico, note que:
(i) f(-12) = 5
(ii) f(-7) = 5
(iii) f(5) = 5
(iv) f(13) = 5

Desejamos resolver a equação f(f(x)) = 5. Temos então as seguintes possibilidades:
(i) f(x) = -12
(ii) f(x) = -7
(iii) f(x) = 5
(iv) f(x) = 13

Como a imagem de f é o intervalo [-5, 16], temos que (i) e (ii) não tem solução.

Já (iii) possui 4 soluções: x=-12, x=-7, x=5, x=13.

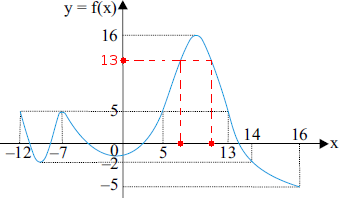
Por fim, temos que (iv) terá 2 soluções. Entretanto, não sabemos exatamente quais são elas. Apenas sabemos que essas soluções estão no intervalo [5, 13]. Vide a figura abaixo.

figura2.png (12.11 KiB) Exibido 11825 vezes

Portanto, temos ao todo 6 soluções para f(f(x)) = 5.