-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478808 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 535694 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499347 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 716964 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2141295 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por rhodry » Qua Nov 16, 2011 18:52
por rhodry » Qua Nov 16, 2011 18:52
Olá pessoal, estou com grande dificuldade de entender fração continua, já pesquisei vários assuntos, mas quando me deparo com as especificações não consigo entender, se alguém puder me dar algumas dicas neste exercício agradeço..
a)Encontre a representação do número ?5 em frações contínuas
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanfx » Qui Nov 17, 2011 01:03
por ivanfx » Qui Nov 17, 2011 01:03
exercício da redefor vou tentar te orientar resolvendo uma outra raiz
Vou pegar
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
com x > 1
De
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
decorre que:
![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png)
racionalizando teremos:
![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
Temos portanto que
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
Ai tu pega o primeiro resultado obtido, ou seja,
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
é um número compreendido entre 4 e 5, portanto
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
com y > 1
De
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
decorre que
![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
resumindo
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
Fazendo a substituição no passo 2 teremos
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
Note que x = y =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, se fossemos continuar o processo de y, encontrariamos w =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
e encontrariamos z =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, e assim sucessivamente em um processo infinito. Segue portanto, que a fração contínua que representa
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
será:
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)
é isso. tente entender, qualquer dúvida volte a perguntar
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por rhodry » Qui Nov 17, 2011 17:03
por rhodry » Qui Nov 17, 2011 17:03
ivanfx escreveu:exercício da redefor vou tentar te orientar resolvendo uma outra raiz
Vou pegar
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
com x > 1
De
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
decorre que:
![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png)
racionalizando teremos:
![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
Temos portanto que
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
Ai tu pega o primeiro resultado obtido, ou seja,
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
é um número compreendido entre 4 e 5, portanto
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
com y > 1
De
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
decorre que
![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
resumindo
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
Fazendo a substituição no passo 2 teremos
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
Note que x = y =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, se fossemos continuar o processo de y, encontrariamos w =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
e encontrariamos z =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, e assim sucessivamente em um processo infinito. Segue portanto, que a fração contínua que representa
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
será:
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)
é isso. tente entender, qualquer dúvida volte a perguntar
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por rhodry » Qui Nov 17, 2011 17:05
por rhodry » Qui Nov 17, 2011 17:05
Olá Colega, estou grato pela dica que vc, me deu,,,, ajudou me muito... consegui esclarecer minhas dúvidas .abraço
-
rhodry
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Out 25, 2011 17:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Rosana Vieira » Sex Nov 18, 2011 12:40
por Rosana Vieira » Sex Nov 18, 2011 12:40
olá como eu faço para encontra as 3 primeiras frações reduzidas de ?5
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanfx » Sex Nov 18, 2011 12:58
por ivanfx » Sex Nov 18, 2011 12:58
Rosana Vieira escreveu:olá como eu faço para encontra as 3 primeiras frações reduzidas de ?5
A equação reduzida você trabalha com a resposta que você obteve quando encontrou a continua, vou utilizar a contínua que calculei, só não irei fazer todos os calculos porque só tenho 15 minutos de intervalo.
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)
a primeira fração reduzida seria calcular
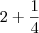
a segunda fração reduzida seria calcular
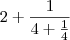
e a terceira fração reduzida seria calcular
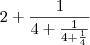
Se calcular essas contas que passei vc obtém as frações reduzidas, caso ainda tenha dúvida avise, voltarei as 15:40 e terei uma aula de folga.
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Rosana Vieira » Sex Nov 18, 2011 14:55
por Rosana Vieira » Sex Nov 18, 2011 14:55
Olá se alguém sober como montar a fração continua da ?5 me ajuda, pois estou com dúvida
2+1
4 + 1
4 + 1
4 + 1
4 + 1/4
2 + 1
4 + 1
4 + 1/4
não conseguir
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Rosana Vieira » Sex Nov 18, 2011 15:01
por Rosana Vieira » Sex Nov 18, 2011 15:01
será que eu fiz certo a fração continua de ?5 eu tentei pela ?7
?5 = 2+1/x
?5 - 2 = 1/x
x = 1/?5 - 2
x= ?5 - 2
?5 - 2 é um número entre 4 e 5, portanto ?5 + 2 = 2+ 1/y, y > 2
?5 + 2 = 4 + 1/y
?5 + 2 - 4= 1/y
?5 - 2= 1/y
y= ?5 + 2
subs.
?5 = 2+1
4+1/?5 + 2
continuando o processo
w=?5 + 2 e z= ?5 + 2
portanto a fração continua será
?5 = 2+ 1
4 + 1
4 + 1
4 + 1
.........
Será isto
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por ivanfx » Sex Nov 18, 2011 15:14
por ivanfx » Sex Nov 18, 2011 15:14
acredito que tenha encontrado dessa forma
![\sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/639ca9de055d9801c6be7eda9464f674.png)
olha, aprenda a utilizar o editor de fórmulas, não é difícil, assim quando postar equações ou fórmulas fica mais fácil de entender, eu achava que era difícil, mas fui obrigado a aprender em um fórum que participo fora do país, ai administrador consertava pra mim, mas vivia dizendo que não consertaria, ai tentei e ficou mais fácil. Sua resposta está correta sim
-
ivanfx
- Usuário Dedicado

-
- Mensagens: 43
- Registrado em: Dom Out 16, 2011 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Rosana Vieira » Sex Nov 18, 2011 16:54
por Rosana Vieira » Sex Nov 18, 2011 16:54
Será que as 3 primeiras frações continuas de ?5 isso
?5 = 2 + 1 (4 + 1/4) seria a primeira
2+ 1 ( 4+ 1/4) = 9/4 segunda
2+ 1(16 + 9/4)= 25/4 terceira
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por matheus_vitorf » Qua Jul 26, 2017 15:31
por matheus_vitorf » Qua Jul 26, 2017 15:31
ivanfx escreveu:exercício da redefor vou tentar te orientar resolvendo uma outra raiz
Vou pegar
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
com x > 1
De
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
decorre que:
![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png)
racionalizando teremos:
![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
Temos portanto que
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
Ai tu pega o primeiro resultado obtido, ou seja,
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
é um número compreendido entre 4 e 5, portanto
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
com y > 1
De
![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png)
decorre que
![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
resumindo
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
Fazendo a substituição no passo 2 teremos
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
Note que x = y =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, se fossemos continuar o processo de y, encontrariamos w =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
e encontrariamos z =
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png)
, e assim sucessivamente em um processo infinito. Segue portanto, que a fração contínua que representa
![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png)
será:
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)
é isso. tente entender, qualquer dúvida volte a perguntar
Olá, e se acontecer de nessa parte, for menor que 1?
![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png)
com x > 1
Eu comecei a fazer a do

:
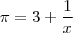
com

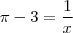
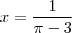
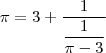
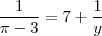
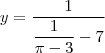


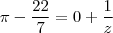
Dá pra ver que não dá
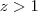
. Como que eu faço?
-
matheus_vitorf
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jul 24, 2017 21:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Frações] Regra de frações
por raymondtfr » Dom Nov 02, 2014 16:49
- 4 Respostas
- 2806 Exibições
- Última mensagem por Russman

Dom Nov 02, 2014 23:57
Aritmética
-
- Função continua
por Amparo » Dom Mar 09, 2008 16:14
- 1 Respostas
- 3577 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:52
Funções
-
- proporçao continua
por hevhoram » Qua Jun 16, 2010 22:19
- 2 Respostas
- 1825 Exibições
- Última mensagem por hevhoram

Qua Jun 16, 2010 23:42
Álgebra Elementar
-
- Funções Continua
por CloudP4 » Qui Jun 24, 2010 00:02
- 1 Respostas
- 1421 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 02:57
Cálculo: Limites, Derivadas e Integrais
-
- função continua
por alexandreredefor » Dom Jul 17, 2011 18:23
- 4 Respostas
- 2512 Exibições
- Última mensagem por Molina

Seg Jul 18, 2011 11:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 32 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\sqrt[]{7} \sqrt[]{7}](/latexrender/pictures/e98da293bc2acc033fbd6f3d1e34f7ab.png) , a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim
, a primeira coisa é descobrir o resultado da raíz está entre quais números inteiros. evidente que está entre 2 e 3, então escreveremos assim![\sqrt[]{7}= 2 + \frac{1}{x} \sqrt[]{7}= 2 + \frac{1}{x}](/latexrender/pictures/dc449225e2ee910d857a4a1198a088dc.png) com x > 1
com x > 1![\sqrt[]{7}- 2 = \frac{1}{x} \sqrt[]{7}- 2 = \frac{1}{x}](/latexrender/pictures/a2200a1972c4eb175e43e9481711087a.png)
![x = \frac{1}{\sqrt[]{7}- 2} x = \frac{1}{\sqrt[]{7}- 2}](/latexrender/pictures/e703f7c2416ddf47e08bf87c1d414070.png) racionalizando teremos:
racionalizando teremos: ![x = \sqrt[]{7}+ 2 x = \sqrt[]{7}+ 2](/latexrender/pictures/ba605a63f7946c831a78007188f2a3e8.png)
![\sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2} \sqrt[]{7}= 2 + \frac{1}{\sqrt[]{7}+ 2}](/latexrender/pictures/8434073fab6ba9d958ac1eec08c01c00.png)
![\sqrt[]{7}+ 2 \sqrt[]{7}+ 2](/latexrender/pictures/0cc3554efec45e0f16ae345feb97811d.png) é um número compreendido entre 4 e 5, portanto
é um número compreendido entre 4 e 5, portanto![\sqrt[]{7}+ 2 = 4 + \frac{1}{y} \sqrt[]{7}+ 2 = 4 + \frac{1}{y}](/latexrender/pictures/b79d9a561619d9b9ce85bed38d372911.png) com y > 1
com y > 1![\sqrt[]{7}+ 2 - 4 = \frac{1}{y} \sqrt[]{7}+ 2 - 4 = \frac{1}{y}](/latexrender/pictures/d745d7b5ba75d3caffe8c114c4fbdca5.png)
![\sqrt[]{7} - 2 = \frac{1}{y} \sqrt[]{7} - 2 = \frac{1}{y}](/latexrender/pictures/53a2f29e9860608c52b9caf2d7b47658.png)
![y = \sqrt[]{7}+ 2 y = \sqrt[]{7}+ 2](/latexrender/pictures/ab850b6eaca21bbe50e1e5e6c6b1cf31.png)
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{\sqrt[]{7}+ 2}}](/latexrender/pictures/e657bf4358b8934ea1d4cca81905a1fc.png)
![\sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{7}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/313a4f31c2a37f96b5b93a6fa1c58a9d.png)


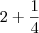
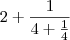
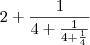
![\sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}} \sqrt[]{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \frac{1}{...}}}}](/latexrender/pictures/639ca9de055d9801c6be7eda9464f674.png)
 :
: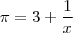 com
com 
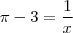
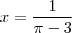
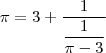
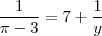
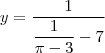


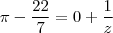
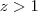 . Como que eu faço?
. Como que eu faço?