O vertice da parabola y= ax2 + bx + c e o ponto (-2,3). Sabendo que 5 e a ordenada onde a curva corta o eixo vertical, podemos afirmar que
(A) a>1, b<1 e c<4
(B) a>2, b>3 e c>4
(C) a<1, b<1 e c>4
(D) a<1, b>1 e c>4
(E) a<1, b<1 e c<4
________________________________________________________________________________________________
Bom, para mim, só falta o valor do b. Olha como eu fiz:
Bom, Tracei o grafico, e marquei os pontos (-2,3) e deu no quarto quadrante. Bom, 5 é o valor de "c" pois é o valor em que corta o eixo de y, certo? com isso ele cortando o y num valor positivo de 5, então para ser uma função, a lógica é que a concavidade é voltada para baixo, então "a" é negativo, ou seja a<1. Agora o "c" --> Como o valor que corta o eixo y é 5, eu acho que o "c" é 5, portanto c>4. Agora eu fico na duvida de como achar o "b". Obg e aguardo resposta!
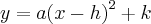em que (h,k) são as coordenadas do vertice da parabola.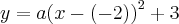
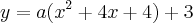
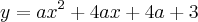(1)
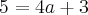
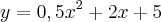onde está muito claro os valores de a, b e c.
.
