 por fernandocez » Qui Mar 10, 2011 22:17
por fernandocez » Qui Mar 10, 2011 22:17
Eu achei que sabia fazer essa, mas depois de comecei a resolver apareceu uma situação que não consegui dar continuidade.
52. O valor mínimo da função
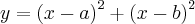
é:
resp.
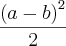
Quando ví o "o valor mínimo" já até imaginei - delta/4a.
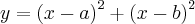
= y=x²-2xa+a²+x²-2xb+b² ?
Aí que vi que tinha a e b e eu não sei o que fazer. Aguardo ajuda obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 10, 2011 22:30
por LuizAquino » Qui Mar 10, 2011 22:30
Dica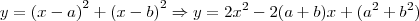
Sabemos que o mínimo (ou máximo) da função
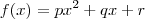
é
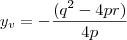
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Qui Mar 10, 2011 23:12
por Fabricio dalla » Qui Mar 10, 2011 23:12
LuizAquino vc poderia resolver a questao de funçao modular com inequaçao pra mim no outro topico ?? desde ja agradeço!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Mar 10, 2011 23:26
por LuizAquino » Qui Mar 10, 2011 23:26
Fabricio dalla escreveu:vc poderia resolver a questao de funçao modular com inequaçao pra mim no outro topico ?
Por favor, não use um tópico aberto para pedir que um outro exercício seja resolvido.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Sex Mar 11, 2011 00:24
por fernandocez » Sex Mar 11, 2011 00:24
LuizAquino escreveu:Dica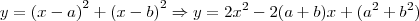
Sabemos que o mínimo (ou máximo) da função
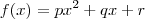
é
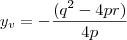
.
Vê por favor Luiz se substitui corretamente. Dei uma simplificada e ficou assim:
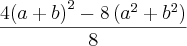
Tentei resolver mas não cheguei na resposta.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Sex Mar 11, 2011 10:38
por LuizAquino » Sex Mar 11, 2011 10:38
Vê por favor Luiz se substitui corretamente. Dei uma simplificada e ficou assim:
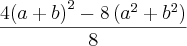
Você esqueceu do sinal de menos antes da fração.
Para terminar a questão, lá vai mais duas dicas:
(i) Divida tanto o numerador quanto o denominador por 4.
(ii) Desenvolva o produto notável
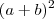
e faça as devidas simplificações no numerador.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Sex Mar 11, 2011 11:17
por fernandocez » Sex Mar 11, 2011 11:17
LuizAquino escreveu:Você esqueceu do sinal de menos antes da fração.
Para terminar a questão, lá vai mais duas dicas:
(i) Divida tanto o numerador quanto o denominador por 4.
(ii) Desenvolva o produto notável
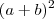
e faça as devidas simplificações no numerador.
Consegui terminar, é o sinal também tava errado, tenho que ter mais atenção, sempre erro os sinais ou esqueço. Tá perto da prova ai vai aumentando a anciedade tenho que estudar a parte pedagógica e português. Obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso (função) 2
por fernandocez » Sáb Mar 19, 2011 18:50
- 2 Respostas
- 1589 Exibições
- Última mensagem por fernandocez

Seg Mar 21, 2011 00:36
Funções
-
- Questão prova concurso função 1
por fernandocez » Ter Mar 22, 2011 09:28
- 6 Respostas
- 2667 Exibições
- Última mensagem por fernandocez

Ter Mar 22, 2011 12:45
Funções
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3563 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2505 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9294 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
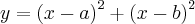 é:
é: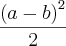
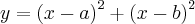 = y=x²-2xa+a²+x²-2xb+b² ?
= y=x²-2xa+a²+x²-2xb+b² ?
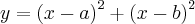 é:
é: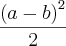
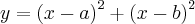 = y=x²-2xa+a²+x²-2xb+b² ?
= y=x²-2xa+a²+x²-2xb+b² ?
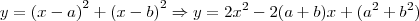
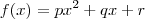 é
é 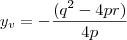 .
.


é
.
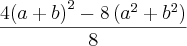

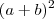 e faça as devidas simplificações no numerador.
e faça as devidas simplificações no numerador.
e faça as devidas simplificações no numerador.
