-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477934 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529932 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493505 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 700311 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2111769 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por matematicada » Qui Nov 25, 2010 11:52
por matematicada » Qui Nov 25, 2010 11:52
No desenvolvimento de
{(x+ \frac{1}{x})}^{12}
, segundo potências
decrescentes de x, o termo independente ocupa a posição de
ordem :
(A) 4.
(B) 6.
(C) 7.
(D) 8.
(E) 5.
obrigada!!!!!
-
matematicada
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Nov 24, 2010 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: turismo
- Andamento: formado
 por alexandre32100 » Qui Nov 25, 2010 13:07
por alexandre32100 » Qui Nov 25, 2010 13:07
Assim, o termo que procuramos é o que não apresenta

. Para isso precisamos de algo como
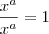
neste.
Lembre-se que o

-ésimo termo de uma expansão de grau

-
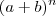
- é
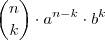
.
Como queremos
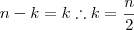
, com

,
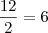
. Assim o termo que procuramos é o
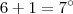
.
-
alexandre32100
-
 por Elcioschin » Qui Nov 25, 2010 16:11
por Elcioschin » Qui Nov 25, 2010 16:11
Pode-se também usar a fórmula do desenvolvimento de (a + b)^n:
Tp+1 = C(n, p)*(b^p)*a^(n-p) -----> a = x, b = 1/x
Tp+1 = C(12, p)*(1/x^p)*x^(12-p)
Tp+1 = C(12, p)*x^(12-2p)
Para ser independente de x -----> 12 - 2p = 0 ----> p = 6
T6+1= C(12, p)*(1/x^p)*x^(n-p)
T6+1 = C(12, 6)
T6+1 = 924
Alternativa C
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Urgente
por jean » Ter Nov 25, 2008 18:39
- 2 Respostas
- 2174 Exibições
- Última mensagem por jean

Ter Nov 25, 2008 21:36
Pedidos
-
- urgente!!
 por weverton » Qui Jul 29, 2010 19:38
por weverton » Qui Jul 29, 2010 19:38
- 4 Respostas
- 3292 Exibições
- Última mensagem por weverton

Sáb Jul 31, 2010 22:47
Estatística
-
- urgente
 por karenblond » Sex Mai 18, 2012 20:17
por karenblond » Sex Mai 18, 2012 20:17
- 1 Respostas
- 1692 Exibições
- Última mensagem por ricardosanto

Sex Mai 18, 2012 21:56
Funções
-
- urgente
por fna » Sex Mai 24, 2013 03:21
- 0 Respostas
- 1339 Exibições
- Última mensagem por fna

Sex Mai 24, 2013 03:21
Álgebra Elementar
-
- Urgente :(
 por m_trulsen » Dom Mar 01, 2015 18:56
por m_trulsen » Dom Mar 01, 2015 18:56
- 0 Respostas
- 1106 Exibições
- Última mensagem por m_trulsen

Dom Mar 01, 2015 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Para isso precisamos de algo como
. Para isso precisamos de algo como 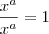 neste.
neste. -ésimo termo de uma expansão de grau
-ésimo termo de uma expansão de grau  -
- 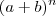 - é
- é 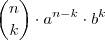 .
.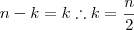 , com
, com  ,
, 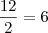 . Assim o termo que procuramos é o
. Assim o termo que procuramos é o 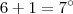 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)