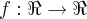 é uma função afim crescente de raiz r < 0,
é uma função afim crescente de raiz r < 0, 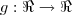 é uma função linear decrescente e
é uma função linear decrescente e 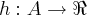 é uma função definida por
é uma função definida por ![h(x) = \frac{1}{\sqrt[]{-{[f(x)]}^{20}}.{[g(-x)]}^{7}} h(x) = \frac{1}{\sqrt[]{-{[f(x)]}^{20}}.{[g(-x)]}^{7}}](/latexrender/pictures/4529488c0d42a216fe58a5890bcad88f.png) , então, o conjunto A, mais amplo possível, é dado por:
, então, o conjunto A, mais amplo possível, é dado por:a) ]r, 0[
b) ]r,
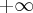 [ - {0}
[ - {0}c) ]
 , 0[ - {r}
, 0[ - {r}d) ]
 , 0[
, 0[Gabarito: c)
Comecei a resolver o exercício anotando os dados das funções
f(x) = ax + b
a > 0 pois o exercício afirmou que a função é crescente
r < 0 (a raiz é negativa)
e g(x) = mx
o coeficiente linear é nulo, portanto, a função é linear
m < 0 pois o exercício afirmou que a função é decrescente.
Chamei o coeficente angular de g de ''m'' para diferenciar da função f.
Depois, percebi que o denominador
![\sqrt[]{-{[f(x)]}^{20}}.{[g(-x)]}^{7}} > 0 \sqrt[]{-{[f(x)]}^{20}}.{[g(-x)]}^{7}} > 0](/latexrender/pictures/c13f4a2b74b1410d971768ae58883c6d.png) (o denominador deve ser maior que zero uma vez que no conjunto dos números reais eu não posso ter uma raiz quadrada com o radicando negativo e também não posso ter um denominador nulo).
(o denominador deve ser maior que zero uma vez que no conjunto dos números reais eu não posso ter uma raiz quadrada com o radicando negativo e também não posso ter um denominador nulo).Consultei ao livro do Iezzi e lá ele fala sobre inequações do tipo
![{[f(x)]}^{n} {[f(x)]}^{n}](/latexrender/pictures/cc728ce87e0350ef4c48476e84cfc37d.png) e relembra a regra de potência: ''toda potência de base real e expoente ímpar conserva o sinal da base'' e ''toda potência de base real e expoente par é um número não negativo''.
e relembra a regra de potência: ''toda potência de base real e expoente ímpar conserva o sinal da base'' e ''toda potência de base real e expoente par é um número não negativo''.A partir daí, não sei como chegar a uma resposta.
Se alguém puder resolver, passo a passo, essa questão eu agradeço. Quero muito entendê-la.
Desde já, agradeço.
OBS: a raiz do denominador abrange todo ele, não consegui fazer com que a raiz se estendesse até o {{[g(-x)]}^{7}}


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.