 por flavio2010 » Dom Jul 18, 2010 19:42
por flavio2010 » Dom Jul 18, 2010 19:42
Dada a função definida para x real positivo, tal que y=x^2, considere o intervalo fechado [a,b] de ponto médio 2 e amplitude A e a imagem desse intervalo, de amplitude B. A razão A/B vale:
a) 1/4
b) 1/6
c) 1/9
d) 1/3
e) 2/9
-
flavio2010
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jun 10, 2010 22:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Tom » Dom Jul 18, 2010 23:31
por Tom » Dom Jul 18, 2010 23:31
Se

é ponto médio do intervalo, então:
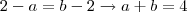
A amplitude do intervalo dos elementos do domínio vale
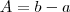
e a amplitude da imagem será
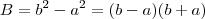
Assim a razão
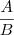
vale :
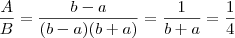
LETRA A
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2858 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 5004 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 2029 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 2021 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
-
- Parábola
por pmfae » Dom Mai 15, 2011 20:55
- 1 Respostas
- 1426 Exibições
- Última mensagem por LuizAquino

Seg Mai 16, 2011 20:37
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é ponto médio do intervalo, então:
é ponto médio do intervalo, então: 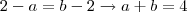
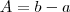 e a amplitude da imagem será
e a amplitude da imagem será 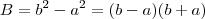
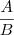 vale :
vale : 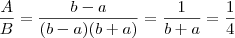


 .
.



