Dada a função do segundo grau f(x)=x^2+m^2x+m^2+1 definida para todo x real e, sendo m um número real e difernete de zero podemos garantir que o gráfico cartesiano desta função:
a) corta o eixo das abscissas.
b) não corta o eixo das abscissas.
c) corta o eixo das abscissas em dois pontos cujas as abscissas tem o mesmo sinal.
d) corta o eixo das abscissas em dois pontos cujas as abscissas tem sinais contrários.
e) pode não cortar o eixo das abscissas ou,se o fizer será em pontos de abscissas nagativa.


 tem raízes reais:
tem raízes reais: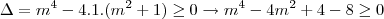 e decorre em
e decorre em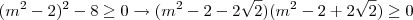
 , a equação
, a equação 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.