Estou com uma duvida em mais uma questão de funções e não sei o que fazer hehe.
Tenho prova amanhã e só faltam algumas coisas pra eu me sentir preparado totalmente pra fazer uma boa prova

e essa

Obrigado ai pra quem puder me ajudar!




 é uma exponencial, ela tem a forma
é uma exponencial, ela tem a forma  , onde k é constante. Usando o gráfico:
, onde k é constante. Usando o gráfico:  . Uma vez obtida a constante, temos que
. Uma vez obtida a constante, temos que  . Portanto,
. Portanto,  . A função inversa é o logaritmo na base a, ou seja,
. A função inversa é o logaritmo na base a, ou seja,  , onde
, onde 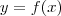 .
.
 , porém
, porém  . Terceira afirmação também é verdadeira pois é uma consequência direta da primeira.
. Terceira afirmação também é verdadeira pois é uma consequência direta da primeira. no intervalo
no intervalo ![[0,3] [0,3]](/latexrender/pictures/ed9c05fe24c0f49f5d73f494a921e0c4.png) é uma parábola (exceto no ponto 2) com raízes 0 e 3. Assim, de [0,3] a função toma a forma de
é uma parábola (exceto no ponto 2) com raízes 0 e 3. Assim, de [0,3] a função toma a forma de  . Agora vamos calcular o limite:
. Agora vamos calcular o limite:  . Portanto, o limite existe.
. Portanto, o limite existe.



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

