A desculpa, pensei que tinha conhecimento em calculo.
Nesta questão não foi feita simplificação, foi feita uma derivação, conceito visto disciplinas de calculo.
A derivada é utilizada, neste caso, para nos fornecer a tangente à f(x) de forma generica, ou seja, achamos (-6x² - 24x + 30) que é o valor da tangente pra todo "x".
No entanto, como o assunto é desconhecido, vou tentar abordar de outra forma, mas recomendo que tu assista no youtube um video sobre derivadas polinomiais ja que é muito util e extremamente simples (MESMO!) de aprender. (
https://www.youtube.com/watch?v=YmtFY6TtAXQ)
Explicação sem derivadas.
As tangentes à uma função são horizontais normalmente nos seus pontos de maximo e minimo (locais), ou seja, no ponto onde a função faz a troca Crescente/Decrescente ou Decrescente/Crescente.
Veja, por exemplo a função seno, onde os pontos azuis representam os maximos e minimos locais e, portanto, pontos de tangente horizontal.
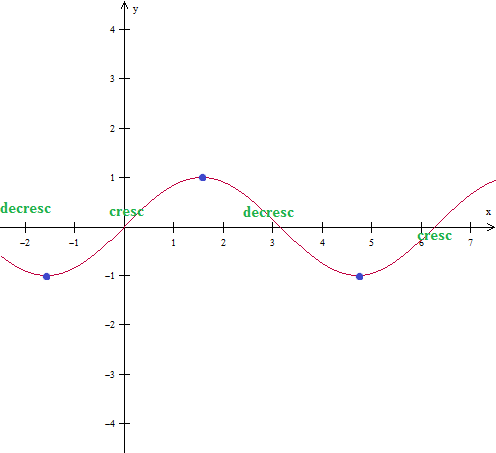
- sen.png (8.85 KiB) Exibido 7329 vezes
Funções de terceiro grau tem um ponto de maximo e outro de minimo, logo precisamos achar estes pontos. Infelizmente funções de terceiro grau não tem uma expressão que dite estes pontos como temos para funções de segundo grau, logo devemos acha-los por tentativa.
Meu conselho, neste caso, seria substituir na função os pontos fornecidos nas alternativas e verificar nos pontos imediatamente anteriores e posteriores se há a mudança de cresc/decresc ou decresc/cresc.
ex.: utiliando os pontos -1 e 5
f(-1) = -30 --> observar os pontos -2 e 0 (anterior e posterior) --> f(-2) = -82 , f(0) = 10
Podemos ver que não ha a mudança, pois de f(-2) para (-1) é cresc e de f(-1) para f(0) é cresc também.
f(5) = -390 --> observar os pontos 4 e 6 (anterior e posterior) --> f(4) = -190 , f(6) = -674
Podemos ver que não ha a mudança, pois de f(-2) para (-1) é decresc e de f(-1) para f(0) é decresc também.
Espero ter ajudado, qualquer coisa mande msg. Bons estudos.









 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.