para q. uma funçao admita funçao inversa,ou seja inversivel é necessario e suficiente q. seja uma funçao bijetiva.
ou seja,seja injetiva e sobrejetiva.seja f,funcao impar;por definiçao f(x)=-f(x),p.qquer x do dominio.
f é injetiva,de fato,pois:
f(x)=-f(x),por ser impar,teremos:
f(x)=-f(x)=f(-(-x))\Rightarrow x=-(-x)...
f é sobrejetiva,de fato,pois:

tal que:
x=-(-x)

y=f(x)=f(-(-x)),sendo f impar teremos:
y=f(x)=f(-(-x))=-f(-x)...



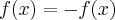 ,por ser impar,teremos:
,por ser impar,teremos:
 tal que:
tal que: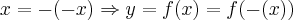 ,sendo f impar teremos:
,sendo f impar teremos:

 tal que:
tal que: y=f(x)=f(-(-x)),sendo f impar teremos:
y=f(x)=f(-(-x)),sendo f impar teremos: