 por adauto martins » Qua Jun 13, 2018 13:16
por adauto martins » Qua Jun 13, 2018 13:16
seja

,definida por:

...mostre que:
a) f nao admite funçao inversa.
b)x,y sao necessariamente numeros irracionais.
soluçao:
a)
seja
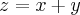
,logo:
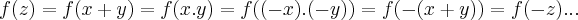
portanto f é uma funçao par,e nao é injetiva(mostre isso),logo nao admite funçao inversa.
b)
seja
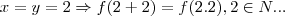
seja
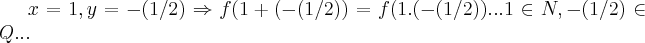
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Jun 14, 2018 13:21
por adauto martins » Qui Jun 14, 2018 13:21
caros colegas do site,
a letra b) que fiz esta incompleta,e com erros.farei uma pequena esplanaçao e logo,qudo puder a resolverei por completo.
pela letra a)sendo f nao injetiva,e portanto nao admite inversa nao podemos ter:
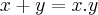
,pois teriamos q. ter:

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Jun 15, 2018 17:03
por adauto martins » Sex Jun 15, 2018 17:03
voltemos a explanaçao,ao tema anterior.
como visto antes,nao podemos ter
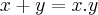
,pois invalidaremos a condiçao de nao existencia da funçao inversa.
logo,necessariamente teremos q. ter
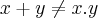
.entao busquemos um
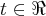
,
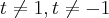
(pq
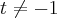
?),tal que
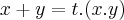
...logo:
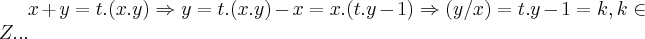
.
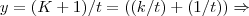
,para q.
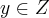
,teriamos q. ter

,ao qual invalidaria a nossa condiçao de nao existencia da inversa...logo, y nao pode ser inteiro...
na mesma deixa,vamos supor que:
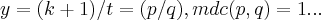
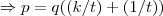
para q.
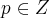
,t teria q. ser igual a um,o q. como visto anteriormente contradiz a condiçao de nao inversa...logo y nao pode ser racional...modo analogo para x...entao x,y teem q. ser irracionais...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolv.funçoes
por adauto martins » Qui Ago 16, 2018 19:29
- 1 Respostas
- 3406 Exibições
- Última mensagem por adauto martins

Qui Ago 16, 2018 19:54
Funções
-
- exercicio resolv.-funçoes
por adauto martins » Ter Jul 31, 2018 20:41
- 1 Respostas
- 3073 Exibições
- Última mensagem por adauto martins

Ter Jul 31, 2018 21:14
Funções
-
- exercicio resolv.equaçoes diofantinas
por adauto martins » Seg Mai 28, 2018 18:49
- 1 Respostas
- 3615 Exibições
- Última mensagem por adauto martins

Seg Jun 04, 2018 19:54
Álgebra Elementar
-
- funções periódicas (exercício do ime de 1995)
por carlospires78 » Ter Out 27, 2009 09:19
- 1 Respostas
- 4911 Exibições
- Última mensagem por BlackFoxes

Sáb Dez 26, 2009 05:08
Funções
-
- [NÃO ENTENDO]EXERCICIO SOBRE FUNÇÕES
por Miya » Qui Mar 05, 2015 16:42
- 3 Respostas
- 5055 Exibições
- Última mensagem por Miya

Sex Mar 13, 2015 12:10
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,definida por:
,definida por: ...mostre que:
...mostre que: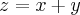 ,logo:
,logo: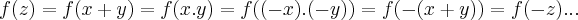
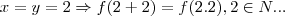
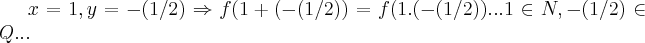

 ,definida por:
,definida por: ...mostre que:
...mostre que: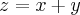 ,logo:
,logo: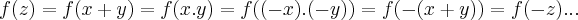
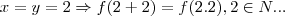
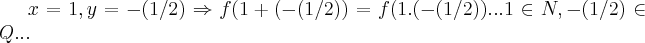

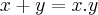 ,pois teriamos q. ter:
,pois teriamos q. ter: ...
...
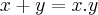 ,pois invalidaremos a condiçao de nao existencia da funçao inversa.
,pois invalidaremos a condiçao de nao existencia da funçao inversa.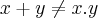 .entao busquemos um
.entao busquemos um 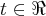 ,
,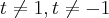 (pq
(pq 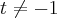 ?),tal que
?),tal que 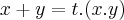 ...logo:
...logo: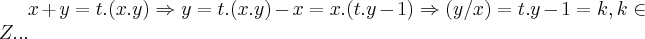 .
.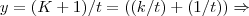 ,para q.
,para q. 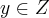 ,teriamos q. ter
,teriamos q. ter  ,ao qual invalidaria a nossa condiçao de nao existencia da inversa...logo, y nao pode ser inteiro...
,ao qual invalidaria a nossa condiçao de nao existencia da inversa...logo, y nao pode ser inteiro...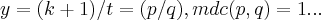
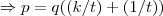
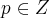 ,t teria q. ser igual a um,o q. como visto anteriormente contradiz a condiçao de nao inversa...logo y nao pode ser racional...modo analogo para x...entao x,y teem q. ser irracionais...
,t teria q. ser igual a um,o q. como visto anteriormente contradiz a condiçao de nao inversa...logo y nao pode ser racional...modo analogo para x...entao x,y teem q. ser irracionais...