 por masterdzs » Ter Mai 15, 2018 22:00
por masterdzs » Ter Mai 15, 2018 22:00
Construa em um sistema de coordenadas cartesianas ortogonais ,o gráfico das seguintes funções :
a) f(x)={2,se x >0
{x+2,se x <0.
b) f(x)={x,se ? x 2
{-1,se 0 ? x < 2
{x - 1 , se x < 0
-
masterdzs
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 15, 2018 21:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Gebe » Ter Mai 15, 2018 23:48
por Gebe » Ter Mai 15, 2018 23:48
Seguem as duas em um intervalo de x entre -20 e 20.
Note que, apesar de parecer pela figura, na questão 1 a função nao esta definida para x=0.
Se houver duvidas mais especificas, mande msg.
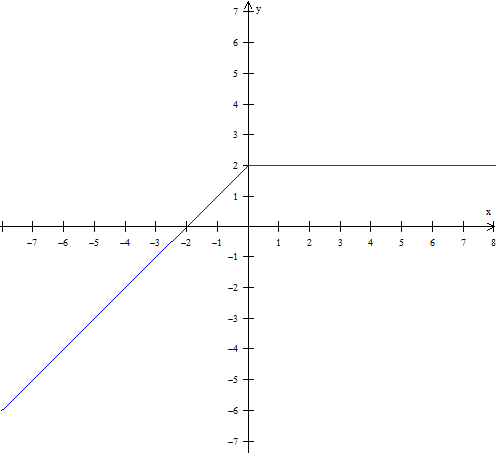
- 1.png (8.03 KiB) Exibido 6368 vezes
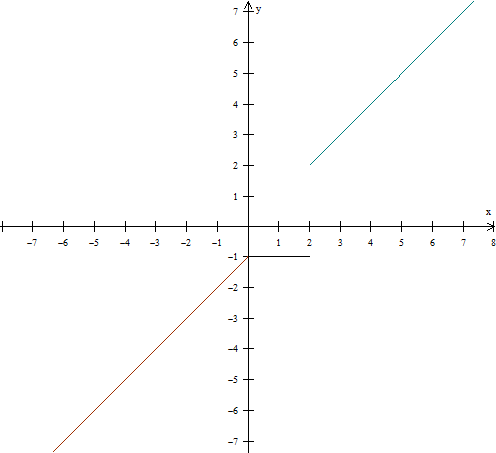
- 2.png (8.5 KiB) Exibido 6368 vezes
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Racional - preciso de ajuda para hoje ainda!
por raf » Seg Set 28, 2015 14:32
- 1 Respostas
- 2607 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:47
Funções
-
- Me ajudem por favor preciso desse trabalho para hoje...ate d
por nda » Sex Dez 12, 2014 07:46
- 2 Respostas
- 3314 Exibições
- Última mensagem por nda

Sex Dez 12, 2014 13:32
Geometria Analítica
-
- [Análise Combinatória] - me ajude, preciso pra amanhã, 11/11
por eduardoferreira » Sáb Nov 10, 2012 23:39
- 7 Respostas
- 5511 Exibições
- Última mensagem por young_jedi

Seg Nov 12, 2012 09:34
Análise Combinatória
-
- [logaritmo] Ajude-me, por favor.
por Cleyson007 » Sáb Mai 17, 2008 23:20
- 4 Respostas
- 12834 Exibições
- Última mensagem por Neperiano

Qui Jun 19, 2008 16:34
Logaritmos
-
- [determinantes] Por favor me ajude!!!
por Cleyson007 » Dom Jul 13, 2008 09:11
- 3 Respostas
- 7184 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 19:46
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



