Ok, antes da resolução em si, algo MUITO IMPORTANTE que talvez tu tenha deixado passar é o conceito de par ordenado. Quando a questão diz (2,6), ela está te dando um par ordenado que pode ser um vertice ou um ponto qualquer da função. O par ordenado é composto por duas coordenadas, X e Y ( ou X e F(X) ), sendo representada na forma (X,Y). Este par nos diz que, para o dado X, a função terá valor F(X) = Y, ou seja, se substituirmos o valor de X por 2, a função terá como resultado F(2) = 6.
Outro conceito importante que tambem esta presente na questão é a ideia de raiz da função. Raiz da função é o numero que quando atribuido a X zera a função, ou seja, se utilizarmos a ideia de par ordenado seria um (X,0) ou F(X) = 0.
Agora para a questão.
Lembre-se que temos uma formula para o vertice da função de 2° grau:
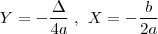
Utilizaremos esta formula mais abaixo.
Com o par (2,6), temos: 4²a + 2b + c = 6
Com a raiz 5, temos: 5²a + 5b + c = 0
Perceba que temos então 2 equações e 3 incognitas, ou seja, ainda precisamos de mais uma equação para poder resolver o sistema de equações. Vamos então utilizar a formula para a coordenada X do vertice.
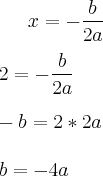
Perceba que agora podemos substituir "b" nas equações por -4a :
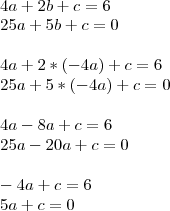
Agora precisamos apenas resolver o sistema de 2 equaçoes com 2 incognitas. Podemos fazer isso, por exemplo, subtraindo a equação 1 da equação 2:

Com o valor do "a", basta substituir nas outras equações para achar "b" e "c"
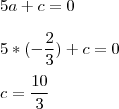

Portanto
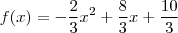
A outra questão vou responder em outra msg assim que puder.
Espero ter ajudado, qualquer duvida mande uma msg. Bons estudos.
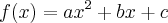 tem vértice no ponto (2,6) e uma raiz no ponto x=5. Determine a expressão de f (ou, em outras palavras, determine os valores dos coeficientes a,b e c .
tem vértice no ponto (2,6) e uma raiz no ponto x=5. Determine a expressão de f (ou, em outras palavras, determine os valores dos coeficientes a,b e c .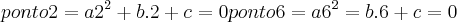
![\frac{-2+-\sqrt[2]{4.4.c}}{2.4} \frac{-2+-\sqrt[2]{4.4.c}}{2.4}](/latexrender/pictures/8a3638fd0d74621bbe2d5d6de210d37d.png) =
=![\frac{-2+-\sqrt[2]{16c}}{8} \frac{-2+-\sqrt[2]{16c}}{8}](/latexrender/pictures/d9f3f748db1ce48a9b7b5d28125bd22f.png) =
= =c=1 e c=-1
=c=1 e c=-1![\frac{-(+6)+-\sqrt[2]{4.36.c}}{2.36} \frac{-(+6)+-\sqrt[2]{4.36.c}}{2.36}](/latexrender/pictures/cf2893562b5a13ffcb4724d99fb632a6.png) =
=![\frac{-6+-\sqrt[2]{144c}}{72} \frac{-6+-\sqrt[2]{144c}}{72}](/latexrender/pictures/a322a8830bd16631e81f13941a68c340.png) =
=![\frac{-6+-\sqrt[2]{{2}^{2}.{2}^{2}.{3}^{2}c}}{72} \frac{-6+-\sqrt[2]{{2}^{2}.{2}^{2}.{3}^{2}c}}{72}](/latexrender/pictures/240b1939d7e047329589f17cdfb06496.png) =
=![\frac{-6+-2.2.3\sqrt[2]{c}}{72} \frac{-6+-2.2.3\sqrt[2]{c}}{72}](/latexrender/pictures/f9c74981a5a5d8172bd947d6d21cdc42.png) =
=![\frac{-6+-12\sqrt[2]{c}}{72}=\frac{6\sqrt[2]{c}}{72} \frac{-6+-12\sqrt[2]{c}}{72}=\frac{6\sqrt[2]{c}}{72}](/latexrender/pictures/4e1a9e6fa92c18f722a89fa2e43bd11f.png) =
=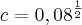 ou c=
ou c=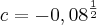
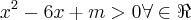 , determine m
, determine m![\frac{6+-\sqrt[2]{4m}}{2} \frac{6+-\sqrt[2]{4m}}{2}](/latexrender/pictures/a0a334f6e1b28af67c405b43ec3f1770.png) =
=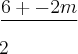 =
=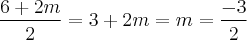 ou
ou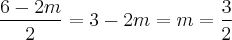


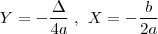
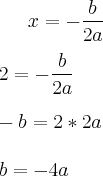
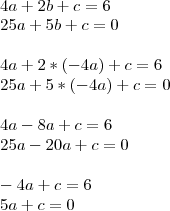

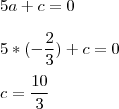

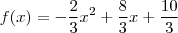
 ) e, portanto, o seu vertice será o ponto mais baixo que ela atinge.
) e, portanto, o seu vertice será o ponto mais baixo que ela atinge. para que Y seja sempre maior que 0.
para que Y seja sempre maior que 0.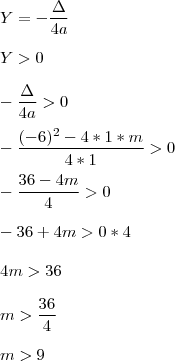

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.