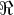 em
em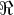 ; dada por
; dada por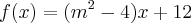 Analise o crescimento/ decrescimento de em função do parâmetro real .
Analise o crescimento/ decrescimento de em função do parâmetro real .resolvi assim mas acho que este cálculo não está correto.
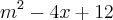 =
=![\frac{-(-4)+-\sqrt[2]{4.1.12}}{2.1} \frac{-(-4)+-\sqrt[2]{4.1.12}}{2.1}](/latexrender/pictures/d98e4d645b1c3a0c7fcd730b57c22ca2.png) =
=![\frac{-(-4)+-\sqrt[2]{48}}{2} \frac{-(-4)+-\sqrt[2]{48}}{2}](/latexrender/pictures/7d46dbc8b20bdbdc5b2e2cbcba4dab7d.png) =
=![\frac{4+-\sqrt[2]{48}}{2} \frac{4+-\sqrt[2]{48}}{2}](/latexrender/pictures/c52fe000c3c5eae96a8a65974ace7b74.png)
![\frac{4+-\sqrt[2]{{2}^{4}.3}}{2} \frac{4+-\sqrt[2]{{2}^{4}.3}}{2}](/latexrender/pictures/d564fb73e9d7334afe530fbb3f0876c8.png) =
=![\frac{4+-2\sqrt[2]{3}}{2} \frac{4+-2\sqrt[2]{3}}{2}](/latexrender/pictures/4a7563328ffd9588e248ae5d371066b3.png) =
=![\frac{6\sqrt[2]{3}}{2} \frac{6\sqrt[2]{3}}{2}](/latexrender/pictures/9bf087b2a3834b7e16988fc77172eb95.png) =
=![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png)
e
![\frac{2\sqrt[2]{3}}{2} \frac{2\sqrt[2]{3}}{2}](/latexrender/pictures/9d8a3b9ca4a19dfc8609a24007e71ee1.png) =
=![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
haverá crescimento da função quando m>0 e decrescimento quando m<0

 em
em ; dada por
; dada por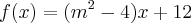 Analise o crescimento/ decrescimento de em função do parâmetro real .
Analise o crescimento/ decrescimento de em função do parâmetro real .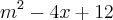 =
=![\frac{-(-4)+-\sqrt[2]{4.1.12}}{2.1} \frac{-(-4)+-\sqrt[2]{4.1.12}}{2.1}](/latexrender/pictures/d98e4d645b1c3a0c7fcd730b57c22ca2.png) =
=![\frac{-(-4)+-\sqrt[2]{48}}{2} \frac{-(-4)+-\sqrt[2]{48}}{2}](/latexrender/pictures/7d46dbc8b20bdbdc5b2e2cbcba4dab7d.png) =
=![\frac{4+-\sqrt[2]{48}}{2} \frac{4+-\sqrt[2]{48}}{2}](/latexrender/pictures/c52fe000c3c5eae96a8a65974ace7b74.png)
![\frac{4+-\sqrt[2]{{2}^{4}.3}}{2} \frac{4+-\sqrt[2]{{2}^{4}.3}}{2}](/latexrender/pictures/d564fb73e9d7334afe530fbb3f0876c8.png) =
=![\frac{4+-2\sqrt[2]{3}}{2} \frac{4+-2\sqrt[2]{3}}{2}](/latexrender/pictures/4a7563328ffd9588e248ae5d371066b3.png) =
=![\frac{6\sqrt[2]{3}}{2} \frac{6\sqrt[2]{3}}{2}](/latexrender/pictures/9bf087b2a3834b7e16988fc77172eb95.png) =
=![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png)
![\frac{2\sqrt[2]{3}}{2} \frac{2\sqrt[2]{3}}{2}](/latexrender/pictures/9d8a3b9ca4a19dfc8609a24007e71ee1.png) =
=![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)

![m^2-4>0\\
\\
m^2>4\\
\\
m>\sqrt[2]{4}\\
\\
\left|m \right|>2\\
\\ m^2-4>0\\
\\
m^2>4\\
\\
m>\sqrt[2]{4}\\
\\
\left|m \right|>2\\
\\](/latexrender/pictures/937607a463130e76c4059a87350cc6b6.png)
![m^2-4<0\\
\\
m^2<4\\
\\
m<\sqrt[2]{4}\\
\\
\left|m \right|<2\\
\\ m^2-4<0\\
\\
m^2<4\\
\\
m<\sqrt[2]{4}\\
\\
\left|m \right|<2\\
\\](/latexrender/pictures/ae1132993ea7fb20effe67f32463849b.png)
![m^2-4=0\\
\\
m^2=4\\
\\
m=\sqrt[2]{4}\\
\\
\left|m \right|=2\\
\\ m^2-4=0\\
\\
m^2=4\\
\\
m=\sqrt[2]{4}\\
\\
\left|m \right|=2\\
\\](/latexrender/pictures/0cefa810c6d6c1109ae221fd3d3e8aac.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.