Olá!
xaxace escreveu:Alguém pode me dar uma luz com essa questão? Não entendi o que ela realmente quer.
A contribuição cobrada por determinada empresa de previdência privada para o trabalhador que ganha de 15 a 20 salários mínimos é dada pela função: f(x) = 0,10 x. Utilizando o salário mínimo de R$ 350,00 construa uma tabela com três pontos onde “x” varie de 15 a 18 salários mínimos e represente a situação graficamente.
Farei apenas UM ponto e o restante é com você!
Vou considerar x = 15 salários, afinal, está compreendido entre 15 e 18. Ademais, de acordo com o enunciado, sabemos que o salário a ser considerado é de R$ 350,00; assim, temos que, 15 salários correspondem a:
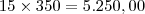
Segue,
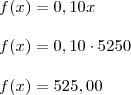
Bom! até aqui devemos marcar no plano cartesiano o ponto (15, 525). Agora é com você... Podes considerar x = 16, x = 17 ou x = 18; por conseguinte, basta determinar quanto isto vale em reais e depois encontrar f(x) e representar no gráfico.
Espero ter ajudado!
Qualquer dúvida, comente!!


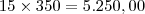
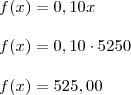

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.