Essa aqui é uma dúvida teórica, talvez seja trivial para alguns. A dúvida é sobre funções que são definidas pelo quociente de funções trigonométricas, na qual deparei e que pode esclarecer algumas dúvidas de outras pessoas.
Deixe-me entrar no contexto dessa dúvida: Suponhamos que desejamos desenhar o gráfico da seguinte função:
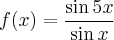
Naturalmente, pensei: essa função não é definida para x = 0, pois vai gerar uma indeterminação 0/0. Entretanto, se desenhar o gráfico da
em algum software, verá que isso não é verdade, pois a função tomará seguinte valor:
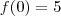
Depois vi que a função
pode ser escrita da seguinte maneira: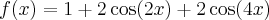
.Ou seja, dessa ultima expressão, fica claro que a função esta definida no valor x = 0.
Então fica claro que deve-se tomar muito cuidado em analisar tais funções. O que gostaria de entender é o seguinte: Como de fato isso acontece? Como que a divisão entre dois numeros nulos se tornam aquele 5?
grato
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.