 por lumbrjack » Ter Mar 01, 2016 13:09
por lumbrjack » Ter Mar 01, 2016 13:09
Pessoal
Estou implementando uma rede neural e tem uma função existente no livro que estou utilizando para a pesquisa, em que estou em dúvidas de como executar sua álgebra. Creio que seja uma multiplicação de matrizes com variáveis.
Esta fórmula esta relacionada com a taxa de aprendizado de uma rede neural. segue a notação:
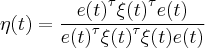
Lembrando que
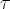
não é exponenciação e sim referente a matrizes.
Alguem poderia me explicar com maiores detalhes como executar essas operações?
obrigado
-
lumbrjack
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 01, 2016 12:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA ELÉTRICA
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Interpretação da notação da função derivada]
 por Jhenrique » Qui Jul 26, 2012 20:27
por Jhenrique » Qui Jul 26, 2012 20:27
- 9 Respostas
- 4386 Exibições
- Última mensagem por Russman

Seg Jul 30, 2012 04:15
Cálculo: Limites, Derivadas e Integrais
-
- [ED] Notação
por Jhenrique » Sex Mai 10, 2013 17:25
- 0 Respostas
- 1466 Exibições
- Última mensagem por Jhenrique

Sex Mai 10, 2013 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Notação de Intervalo
por Luanna » Seg Mar 29, 2010 23:56
- 2 Respostas
- 7981 Exibições
- Última mensagem por Luanna

Ter Mar 30, 2010 00:14
Álgebra Elementar
-
- Dúvida em Notação
por dsilvavinicius » Dom Jul 18, 2010 15:55
- 1 Respostas
- 1927 Exibições
- Última mensagem por dsilvavinicius

Dom Jul 18, 2010 15:59
Geometria Analítica
-
- notação cientifica
por jose henrique » Qui Fev 10, 2011 22:45
- 1 Respostas
- 2508 Exibições
- Última mensagem por Molina

Sex Fev 11, 2011 02:16
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
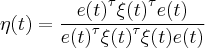
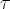 não é exponenciação e sim referente a matrizes.
não é exponenciação e sim referente a matrizes.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.