 por Matpas » Ter Set 22, 2015 10:27
por Matpas » Ter Set 22, 2015 10:27
Amigos, como se resolve o exercício abaixo?
Sabendo que f(x+1) = 2x, quanto vale f(4)?
-
Matpas
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Ago 25, 2015 15:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Ter Out 06, 2015 06:36
por DanielFerreira » Ter Out 06, 2015 06:36
Comparando
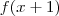
com
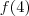
, temos que:
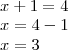
Daí,
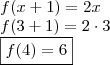
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Matpas » Ter Out 06, 2015 10:04
por Matpas » Ter Out 06, 2015 10:04
Valeu amigo. Obrigado pela ajuda.
-
Matpas
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Ago 25, 2015 15:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3260 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2891 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Dominio] Cálculo 2- Domínio
por Saturnino Nataniel » Seg Fev 25, 2013 14:09
- 2 Respostas
- 1730 Exibições
- Última mensagem por timoteo

Ter Abr 09, 2013 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Domínio x² -4/x - 1
por virginia » Qui Abr 25, 2013 11:21
- 4 Respostas
- 3250 Exibições
- Última mensagem por virginia

Sáb Abr 27, 2013 01:17
Funções
-
- [domínio] Funcões
por Cleyson007 » Qua Out 29, 2008 00:28
- 2 Respostas
- 2374 Exibições
- Última mensagem por Cleyson007

Seg Jun 01, 2009 12:38
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


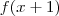 com
com 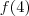 , temos que:
, temos que: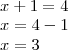
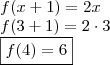


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)