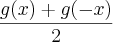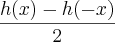por Taah » Sáb Mar 27, 2010 15:33
por Taah » Sáb Mar 27, 2010 15:33
Seja f uma função real. Mostre que existem uma função par 'g' e uma função ímpar 'h' tal que f(x)= g(x) + h(x),

x

Domínio de f. Em particular, determine 'g' e 'h' no caso em que f(x)= ln(

+x+1)
Iniciei esse ano meu curso de Ciencias Exatas e o professor de cálculo diferencial pediu que levássemos a resposta dessa questão e expuséssemos ela em sala de aula para toda a turma, resultado: por mais que eu tente quando chega no meio da questão eu me enrolo toda. Gostaria de ser ajudada se possível!
Desde já agradeço!
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
 por Elcioschin » Sáb Mar 27, 2010 23:27
por Elcioschin » Sáb Mar 27, 2010 23:27
Vou tentar iniciar
f(x) = ln(x² + x + 1) ----> x² + x + 1 = e^f(x)
x² + x + 1 = e^[g(x) + h(x)] ----> (x² + 2x + 1) - x = [e^g(x)]*[e^h(x)] -----> (x + 1)² - (Vx)² = [e^g(x)]*[e^h(x)] ----> (x + 1 + Vx)*(x + 1 - Vx) = [e^g(x)]*[e^h(x)]
x + 1 + Vx = e^g(x) -----> g(x) = ln(x + 1 + Vx)
x + 1 - Vx = e^h(x) -----> h(x) =ln*(x + 1 - Vx)
Falta provar que uma das funções é ímpar e a outra par.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Taah » Dom Mar 28, 2010 12:16
por Taah » Dom Mar 28, 2010 12:16
Vlw
Elcioschin!
Ajudou mto

-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
 por Taah » Dom Mar 28, 2010 13:21
por Taah » Dom Mar 28, 2010 13:21
A prova de que g(x) é par:
g(x) =
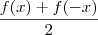
g(-x)=
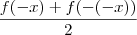
=
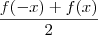
=
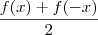
= g(x)
g(-x)= g(x)
A prova de que h(x) é ímpar:
h(x)=
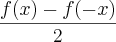
h(-x)=

=
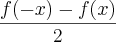
=
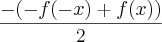
=
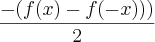
= -h(x)
h(-x)= -h(x)
CORRETO?????
Agora, porque g(x) é uma função definida por:
g(x)=
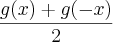
e h(x) é uma função definida por:
h(x)=
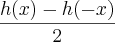
????????????
E não por:
g(-x)= g(x)
e...
h(-x)= -h(x)
??????????????
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto da soma pela diferença - ordem do raciocinio
por Soprano » Qui Mar 03, 2016 09:17
- 3 Respostas
- 2854 Exibições
- Última mensagem por DanielFerreira

Ter Mar 08, 2016 21:47
Polinômios
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3273 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
-
- funcao impar
por irineu junior » Sex Mar 12, 2010 20:49
- 2 Respostas
- 2560 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 20:55
Funções
-
- Função par x ímpar
por Jonatan » Sex Jul 30, 2010 12:39
- 1 Respostas
- 2363 Exibições
- Última mensagem por Molina

Sex Jul 30, 2010 14:31
Funções
-
- Função impar
por rapina » Qua Jan 11, 2012 14:48
- 2 Respostas
- 2251 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 12, 2012 15:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 x
x  Domínio de f. Em particular, determine 'g' e 'h' no caso em que f(x)= ln(
Domínio de f. Em particular, determine 'g' e 'h' no caso em que f(x)= ln( +x+1)
+x+1)



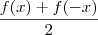
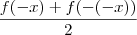 =
= 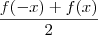 =
= 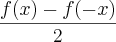
 =
= 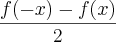 =
= 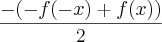 =
=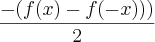 = -h(x)
= -h(x)