![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png) .
.Pois bem, eu fiz uma substituição através de
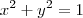 nas equações paramétricas. O problema foi na hora de identificar a trajetória da partícula: quando igualei t a 0, então x=1 e y=0. E quando igualei t a pi, o x também é igual a 1, e y também é zero, ou seja, a medida que aumento o t até fechar o intervalo, eu obtive o mesmo ponto que a partícula deve percorrer, ou seja, ele parte de um ponto, e depois ela volta para o mesmo ponto. E eu não tenho muita certeza se isso está correto ou não. Poderia alguém me explicar a lógica dessa questão? Enfim, quem puder, eu agradeço!
nas equações paramétricas. O problema foi na hora de identificar a trajetória da partícula: quando igualei t a 0, então x=1 e y=0. E quando igualei t a pi, o x também é igual a 1, e y também é zero, ou seja, a medida que aumento o t até fechar o intervalo, eu obtive o mesmo ponto que a partícula deve percorrer, ou seja, ele parte de um ponto, e depois ela volta para o mesmo ponto. E eu não tenho muita certeza se isso está correto ou não. Poderia alguém me explicar a lógica dessa questão? Enfim, quem puder, eu agradeço! Abraço!



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)