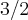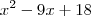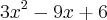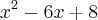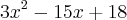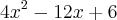por lcsantos85 » Ter Nov 17, 2009 00:58
por lcsantos85 » Ter Nov 17, 2009 00:58
Duvida com essa pergunta, postei o enunciado porque é importante pra determinar a opção certa. Por favor ajudem!
A função f(x) do 2º grau possui uma
raiz que é o dobro da outra e intercepta o
eixo das ordenadas no ponto 8. Sabe-se que
a abscissa do vértice é igual a
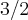
, f(x) é
dada por:
a) f(x)=
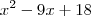
b) f (x) =
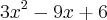
c) f (x) =
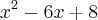
d) f (x) =
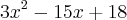
e) f (x) =
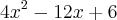
Qual a certa? Explique por favor. Acho que tem que ser anulada porque nenhum alternativa atende as três afirmações. No caso de B ela nao intercepta as ordenadas no ponto 8, no caso de C (raizes 4 e 2) a abcissa do vertice seria 3, não?
Obrigado!
Obrigado!
-
lcsantos85
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Nov 17, 2009 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Egenharia
- Andamento: cursando
 por Elcioschin » Ter Nov 17, 2009 10:35
por Elcioschin » Ter Nov 17, 2009 10:35
y = ax² + bx + c
Raízes: r , s ----> s = 2r ----> A(r, 0) , B(2r, 0)
c = 8
xV = 3/2 ----> xV = (xA + xB)/2 ----> 3/2 = (r + 2r)/2 ----> r = 1 ----> s = 2
r + s = - b/a -----> 1 + 2 = - b/a ----> b = - 3a
r*s = c/a ----> 1*2 = 8/a ----> a = 4 -----> b = -12
y = 4x² - 12x + 8
Acho que deve ser a alternativa E só que deve estar digitada errada
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2288 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2412 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2091 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3448 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2143 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.