visível a partir da Terra, seja dado pela função:
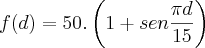
, na qual d é o número de dias
transcorridos a partir de uma data inicial de observação.
Em relação a essa função e ao que ela representa, julgue os
itens a seguir, assinalando (V) para os verdadeiros e (F) para
os falsos.
0.( ) A observação teve início em uma noite de lua cheia.
1.( ) Durante a primeira semana da observação, a Lua
estava em sua fase crescente.
2.( ) No dia tal que d = 60, a lua estará em quarto
crescente.
3.( ) A função está longe da realidade observada, pois o
período lunar representado por ela difere do real por
mais do que dois dias.
4.( ) A lua nova ocorre apenas para d = 22,5.


