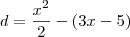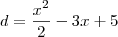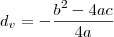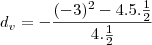Considere os segmentos paralelos ao eixo y, com uma das extremidades sobre o gráfico da função f e a outra extremidade sobre o gráfico da função g. Entre esses segmentos, seja S o que tem o menor comprimento. Assim sendo, o comprimento do segmento S é
a) 1/2 b) 3/4 c) 1 d) 5/4
Me ajudem passo a passo? Obg.