Esse é meu primeiro post nesse fórum. Se eu estiver fazendo alguma coisa errada por favor me avisem, não tive tempo de ler as regras de postagem.
Recebi uma lista com 60 questões que estou tendo dificuldades, mas com a ajuda de vocês, creio que conseguirei tranquilamente.
Eu estou com dúvida no seguinte.
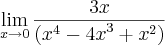
o enunciado diz: Aplicando propriedades de limites e algébricas, calcule cada limite abaixo e avalie sua existência, dizendo se eles existem ou não.
DÚVIDA: Terei que fatorar esse polinômino, correto ? Terei que achar os limites laterais antes ( 0+, 0-) correto ?
pelos meus cálculos
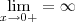 e
e 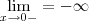 . Isso está correto ?
. Isso está correto ? Att, Fábio Cabral.
ps.: Ingressei neste fórum pois aqui, as pessoas não dão as respostas prontas, mas ensinam


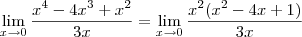
 :
: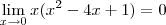


 .
.![\lim_{x\rightarrow0} \frac{3x}{({x}^{4}-{4x}^{3}+{x}^{2})} = \lim_{x\rightarrow0} \frac{3}{({x}^{3}-{4x}^{2}+x)} =\lim_{x\rightarrow0} \left[3 \right].\left[ \frac{1}{({x}^{3}-{4x}^{2}+x)} \right] = +\infty \lim_{x\rightarrow0} \frac{3x}{({x}^{4}-{4x}^{3}+{x}^{2})} = \lim_{x\rightarrow0} \frac{3}{({x}^{3}-{4x}^{2}+x)} =\lim_{x\rightarrow0} \left[3 \right].\left[ \frac{1}{({x}^{3}-{4x}^{2}+x)} \right] = +\infty](/latexrender/pictures/c1392dc14db91455dd3c8e86750e5500.png)

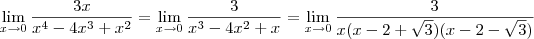
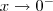 , o produto
, o produto 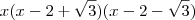 é negativo, logo
é negativo, logo 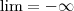 .
.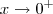 , o produto
, o produto 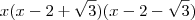 é positivo, logo
é positivo, logo 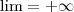 .
.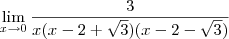

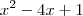 e escrevi na forma fatorada.
e escrevi na forma fatorada.