Problema Com Inequação do Exponencial

por **chenz** » Sáb Jun 19, 2010 17:13

Pessoal, estou com o seguinte problema e não consigo chegar ao resultado:
$\left(\frac{2}{3} \right)^{2x}-\frac{13}{6}*\left(\frac{2}{3} \right)^x+1\geq0$
$\left(\left(\frac{2}{3} \right)^x \right)^2-\frac{13}{6}*\left(\frac{2}{3} \right)^x+1\geq0$
$\left(\frac{2}{3} \right)^x=y$
${y}^{2}-\frac{13}{6}*y+1\geq0$
Multiplicando por 6....
$6*{y}^{2}-13*y+6\geq0$
a=6;b=-13;c=6

$\Delta={b}^{2}-4*a*c$
$\Delta=\left(-13 \right)^2-4*6*6$
$\Delta=25$
$\frac{13\pm5}{12}$
$y''=\frac{3}{2}$
$y'=\frac{2}{3}$
$x'=\left(\frac{2}{3}\right)^\frac{2}{3}$
$x''=\left(\frac{2}{3}\right)^\frac{3}{2}$
Porém a resposta é:
$x'\leq-1$ e
$x''\geq1$

Onde estou errando? A sequencia de cálculo está correta?

Obrigado a todos....

por **Molina** » Sáb Jun 19, 2010 21:31

Boa noite!

Aqui está seu erro:

chenz escreveu: $y''=\frac{3}{2}$
$y'=\frac{2}{3}$
$x'=\left(\frac{2}{3}\right)^\frac{2}{3}$
$x''=\left(\frac{2}{3}\right)^\frac{3}{2}$

Os valores que você encontra são y' e y". Você está substituindo no x e não no y.

Deixe o expoente x como ele está e substitua os valores encontrados após a igualdade, na condição inicial que você mesmo deu.

:y:

por **chenz** » Dom Jun 20, 2010 12:35

Obrigado Diego Molina !!!! Valeu mesmo....Não acreditei que a resposta estava na minha frete....hehehehehehe....Obrigado!!!

Cristiano Henz

Problema Com Inequação do Exponencial

Problema Com Inequação do Exponencial

Problema Com Inequação do Exponencial

Re: Problema Com Inequação do Exponencial

Re: Problema Com Inequação do Exponencial

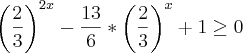
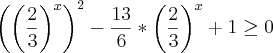
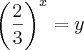
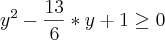
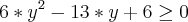
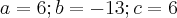
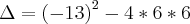
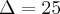
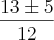
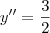
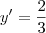
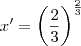
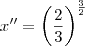
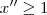
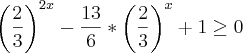
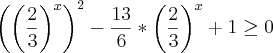
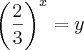
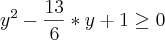
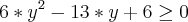
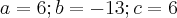
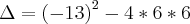
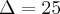
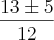
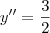
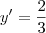
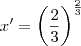
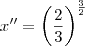
Quem está online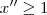